|
|
void | clear () |
| | Reset the projection.
|
| |
|
Vector3 | mkEigenVector (Matrix3 A, const double &lambda) |
| |
|
|
| Sphericity (double rparam=2.0) |
| | Constructor.
|
| |
|
| Sphericity (const FinalState &fsp, double rparam=2.0) |
| |
|
| DEFAULT_RIVET_PROJ_CLONE (Sphericity) |
| | Clone on the heap.
|
| |
|
|
double | sphericity () const |
| | Sphericity.
|
| |
|
double | transSphericity () const |
| | Transverse sphericity.
|
| |
|
double | planarity () const |
| | Planarity.
|
| |
|
double | aplanarity () const |
| | Aplanarity.
|
| |
|
|
const Vector3 & | sphericityAxis () const |
| | Sphericity axis.
|
| |
|
const Vector3 & | sphericityMajorAxis () const |
| | Sphericity major axis.
|
| |
|
const Vector3 & | sphericityMinorAxis () const |
| | Sphericity minor axis.
|
| |
|
| const Vector3 & | axis1 () const |
| |
|
const Vector3 & | axis2 () const |
| | The 2nd most significant ("major") axis.
|
| |
|
const Vector3 & | axis3 () const |
| | The least significant ("minor") axis.
|
| |
|
|
double | lambda1 () const |
| |
|
double | lambda2 () const |
| |
|
double | lambda3 () const |
| |
|
Ways to do the calculation directly, without engaging the caching system
|
|
void | calc (const FinalState &fs) |
| | Manually calculate the sphericity, without engaging the caching system.
|
| |
|
void | calc (const Particles &particles) |
| | Manually calculate the sphericity, without engaging the caching system.
|
| |
|
void | calc (const Jets &jets) |
| | Manually calculate the sphericity, without engaging the caching system.
|
| |
|
void | calc (const vector< FourMomentum > &momenta) |
| | Manually calculate the sphericity, without engaging the caching system.
|
| |
| void | calc (const vector< Vector3 > &momenta) |
| | Manually calculate the sphericity, without engaging the caching system. More...
|
| |
|
virtual | ~AxesDefinition () |
| | Virtual destructor.
|
| |
|
virtual unique_ptr< Projection > | clone () const =0 |
| | Clone on the heap.
|
| |
|
virtual std::string | name () const |
| | Get the name of the projection.
|
| |
|
| Projection () |
| | The default constructor.
|
| |
|
virtual | ~Projection () |
| | The destructor.
|
| |
| bool | before (const Projection &p) const |
| |
| virtual const std::set< PdgIdPair > | beamPairs () const |
| |
| Projection & | addPdgIdPair (PdgId beam1, PdgId beam2) |
| |
|
| ProjectionApplier () |
| | Constructor.
|
| |
|
void | markAsOwned () const |
| | Mark this object as owned by a proj-handler.
|
| |
|
std::set< ConstProjectionPtr > | getProjections () const |
| | Get the contained projections, including recursion.
|
| |
|
bool | hasProjection (const std::string &name) const |
| | Does this applier have a projection registered under the name name?
|
| |
| template<typename PROJ > |
| const PROJ & | getProjection (const std::string &name) const |
| |
| template<typename PROJ > |
| const PROJ & | get (const std::string &name) const |
| |
| const Projection & | getProjection (const std::string &name) const |
| |
| template<typename PROJ > |
| const PROJ & | applyProjection (const Event &evt, const Projection &proj) const |
| | Apply the supplied projection on event evt. More...
|
| |
| template<typename PROJ > |
| const PROJ & | apply (const Event &evt, const Projection &proj) const |
| |
| template<typename PROJ > |
| const PROJ & | applyProjection (const Event &evt, const PROJ &proj) const |
| | Apply the supplied projection on event evt. More...
|
| |
| template<typename PROJ > |
| const PROJ & | apply (const Event &evt, const PROJ &proj) const |
| |
| template<typename PROJ > |
| const PROJ & | applyProjection (const Event &evt, const std::string &name) const |
| |
| template<typename PROJ > |
| const PROJ & | apply (const Event &evt, const std::string &name) const |
| |
| template<typename PROJ > |
| const PROJ & | apply (const std::string &name, const Event &evt) const |
| |
Calculate the sphericity event shape.
The sphericity tensor (or quadratic momentum tensor) is defined as
![\[ S^{\alpha \beta} = \frac{\sum_i p_i^\alpha p_i^\beta}{\sum_i |\mathbf{p}_i|^2} \]](form_108.png)
, where the Greek indices are spatial components and the Latin indices are used for sums over particles. From this, the sphericity, aplanarity and planarity can be calculated by combinations of eigenvalues.
Defining the three eigenvalues 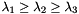 , with
, with 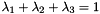 , the sphericity is
, the sphericity is
![\[ S = \frac{3}{2} (\lambda_2 + \lambda_3) \]](form_109.png)
The aplanarity is 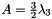 and the planarity is
and the planarity is 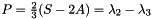 . The eigenvectors define a set of spatial axes comparable with the thrust axes, but more sensitive to high momentum particles due to the quadratic sensitivity of the tensor to the particle momenta.
. The eigenvectors define a set of spatial axes comparable with the thrust axes, but more sensitive to high momentum particles due to the quadratic sensitivity of the tensor to the particle momenta.
Since the sphericity is quadratic in the particle momenta, it is not an infrared safe observable in perturbative QCD. This can be fixed by adding a regularizing power of 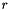 to the definition:
to the definition:
![\[ S^{\alpha \beta} = \frac{\sum_i |\mathbf{p}_i|^{r-2} p_i^\alpha p_i^\beta} {\sum_i |\mathbf{p}_i|^r} \]](form_112.png)
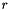 is available as a constructor argument on this class and will be taken into account by the Cmp<Projection> operation, so a single analysis can use several sphericity projections with different
is available as a constructor argument on this class and will be taken into account by the Cmp<Projection> operation, so a single analysis can use several sphericity projections with different 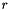 values without fear of a clash.
values without fear of a clash.
 1.8.13
1.8.13
 Public Member Functions inherited from
Public Member Functions inherited from ![\[ S^{\alpha \beta} = \frac{\sum_i p_i^\alpha p_i^\beta}{\sum_i |\mathbf{p}_i|^2} \]](form_108.png)
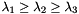 , with
, with 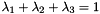 , the sphericity is
, the sphericity is ![\[ S = \frac{3}{2} (\lambda_2 + \lambda_3) \]](form_109.png)
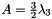 and the planarity is
and the planarity is 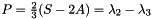 . The eigenvectors define a set of spatial axes comparable with the thrust axes, but more sensitive to high momentum particles due to the quadratic sensitivity of the tensor to the particle momenta.
. The eigenvectors define a set of spatial axes comparable with the thrust axes, but more sensitive to high momentum particles due to the quadratic sensitivity of the tensor to the particle momenta.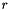 to the definition:
to the definition: ![\[ S^{\alpha \beta} = \frac{\sum_i |\mathbf{p}_i|^{r-2} p_i^\alpha p_i^\beta} {\sum_i |\mathbf{p}_i|^r} \]](form_112.png)