Rivet Namespace Reference
Namespaces | |
| namespace | mT2 |
| namespace | mt2_bisect |
| namespace | PID |
Classes | |
| class | MC_JetAnalysis |
| Base class providing common functionality for MC jet validation analyses. More... | |
| class | Analysis |
| This is the base class of all analysis classes in Rivet. More... | |
| struct | AnaHandleLess |
| class | AnalysisHandler |
| class | AnalysisInfo |
| class | AnalysisLoader |
| Internal class which loads and registers analyses from plugin libs. More... | |
| class | Cmp |
| class | Cmp< Projection > |
| Specialization of Cmp for checking the ordering of two {Projection}s. More... | |
| class | Cmp< double > |
| Specialization of Cmp for checking the ordering of two floating point numbers. More... | |
| class | Event |
| class | Error |
| Generic runtime Rivet error. More... | |
| class | RangeError |
| Error for e.g. use of invalid bin ranges. More... | |
| class | LogicError |
| Error specialisation for places where alg logic has failed. More... | |
| class | PidError |
| Error specialisation for failures relating to particle ID codes. More... | |
| class | WeightError |
| Errors relating to event/bin weights Arises in computing statistical quantities because e.g. the bin weight is zero or negative. More... | |
| class | HistoHandler |
| The projection handler is a central repository for histograms (and other analysis stats objects) to be used in a Rivet analysis run. This eliminates the need for analysis classes to contain large numbers of histogram pointer members, and allows histograms to be accessed via more user-friendly names than C++ variable names allow. More... | |
| class | Jet |
| A minimal class representing a jet of particles. More... | |
| class | LorentzTransform |
| Object implementing Lorentz transform calculations and boosts. More... | |
| class | Matrix3 |
| Specialisation of MatrixN to aid 3 dimensional rotations. More... | |
| class | EigenSystem |
| Handy object containing results of a diagonalization. More... | |
| struct | EigenPairCmp |
| Comparison functor for "eigen-pairs". More... | |
| class | Matrix |
General 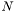 -dimensional mathematical matrix object. More... -dimensional mathematical matrix object. More... | |
| class | Vector3 |
| Three-dimensional specialisation of Vector. More... | |
| class | FourVector |
| Specialisation of VectorN to a general (non-momentum) Lorentz 4-vector. More... | |
| class | FourMomentum |
| Specialized version of the FourVector with momentum/energy functionality. More... | |
| class | Vector |
A minimal base class for 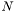 -dimensional vectors. More... -dimensional vectors. More... | |
| class | Particle |
| Representation of particles from a HepMC::GenEvent. More... | |
| class | ParticleBase |
| Base class for particle-like things like Particle and Jet. More... | |
| class | ParticleNames |
| class | Projection |
| Base class for all Rivet projections. More... | |
| class | ProjectionApplier |
| Common base class for Projection and Analysis, used for internal polymorphism. More... | |
| class | ProjectionHandler |
| The projection handler is a central repository for projections to be used in a Rivet analysis run. More... | |
| class | AxesDefinition |
| Base class for projections which define a spatial basis. More... | |
| class | Beam |
| Project out the incoming beams. More... | |
| class | BeamThrust |
| class | CentralEtHCM |
Summed 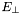 of central particles in HCM system. More... of central particles in HCM system. More... | |
| class | ChargedFinalState |
| Project only charged final state particles. More... | |
| class | ChargedLeptons |
| Get charged final-state leptons. More... | |
| class | ClusteredPhotons |
| Find final state photons which in a cone around any particle in the "signal" final state. More... | |
| class | ConstRandomFilter |
| Functor used to implement constant random lossiness. More... | |
| class | ConstLossyFinalState |
| Randomly lose a constant fraction of particles. More... | |
| class | DISKinematics |
| Get the DIS kinematic variables and relevant boosts for an event. More... | |
| class | DISLepton |
| Get the incoming and outgoing leptons in a DIS event. More... | |
| class | FastJets |
| Project out jets found using the FastJet package jet algorithms. More... | |
| class | FinalState |
| Project out all final-state particles in an event. Probably the most important projection in Rivet! More... | |
| class | FinalStateHCM |
| Final state particles boosted to the hadronic center of mass system. More... | |
| class | FoxWolframMoments |
| Calculate Fox-Wolfram moments. More... | |
| class | FParameter |
| class | HadronicFinalState |
| Project only hadronic final state particles. More... | |
| class | Hemispheres |
| Calculate the hemisphere masses and broadenings. More... | |
| class | IdentifiedFinalState |
| Produce a final state which only contains specified particle IDs. More... | |
| class | InitialQuarks |
Project out quarks from the hard process in  events. More... events. More... | |
| class | InvMassFinalState |
| Identify particles which can be paired to fit within a given invariant mass window. More... | |
| class | IsolationProjection |
| class | JetAlg |
| Abstract base class for projections which can return a set of Jets. More... | |
| class | JetShape |
| Calculate the jet shape. More... | |
| class | LeadingParticlesFinalState |
| Get the highest-pT occurrences of FS particles with the specified PDG IDs. More... | |
| class | ClusteredLepton |
| class | LeptonClusters |
| Cluster photons from a given FS to all charged particles (typically leptons) from signal and store the original charged particles and photons as particles() while the newly created clustered lepton objects are accessible as clusteredLeptons(). More... | |
| class | LossyFinalState |
| Templated FS projection which can lose some of the supplied particles. More... | |
| class | MergedFinalState |
| Get final state particles merged from two FinalState projections. More... | |
| class | MissingMomentum |
Calculate missing 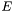 , , 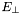 etc. More... etc. More... | |
| class | Multiplicity |
| Count the final-state particles in an event. More... | |
| class | NeutralFinalState |
| Project only neutral final state particles. More... | |
| class | ParisiTensor |
| Calculate the Parisi event shape tensor (or linear momentum tensor). More... | |
| class | PVertex |
| Get the position of the primary vertex of an event. More... | |
| class | Sphericity |
| Calculate the sphericity event shape. More... | |
| class | Spherocity |
| Get the transverse spherocity scalars for hadron-colliders. More... | |
| class | SVertex |
| Determine secondary vertices. More... | |
| class | Thrust |
| Get the e+ e- thrust basis and the thrust, thrust major and thrust minor scalars. More... | |
| class | TotalVisibleMomentum |
Get the total energy vector, allowing missing  etc. to be calculated. More... etc. to be calculated. More... | |
| class | TriggerCDFRun0Run1 |
| Access to the min bias triggers used by CDF in Run 0 and Run 1. More... | |
| class | TriggerCDFRun2 |
| Access to the min bias triggers used by CDF in Run 0 and Run 1. More... | |
| class | TriggerUA5 |
| Access to the min bias triggers used by UA5. More... | |
| class | UnstableFinalState |
| Project out all physical-but-decayed particles in an event. More... | |
| class | VetoedFinalState |
| FS modifier to exclude classes of particles from the final state. More... | |
| class | VisibleFinalState |
| Final state modifier excluding particles which are not experimentally visible. More... | |
| class | WFinder |
| Convenience finder of leptonically decaying Ws. More... | |
| class | ZFinder |
| Convenience finder of leptonically decaying Zs. More... | |
| struct | DPSXPoint |
| Container for x-axis point details. More... | |
| struct | DPSXYPoint |
| Container for x-axis point details. More... | |
| class | Run |
| Interface to handle a run of events read from a HepMC stream or file. More... | |
| class | BinnedHistogram |
| class | Log |
| class | ALEPH_1991_S2435284 |
| ALEPH LEP1 charged multiplicity in hadronic Z decay. More... | |
| class | ALEPH_1996_S3196992 |
| ALEPH measurement of quark-to-photon fragmentation function. More... | |
| class | ALEPH_1996_S3486095 |
| ALEPH QCD study with event shapes and identified particles. More... | |
| class | ALEPH_2004_S5765862 |
| ALEPH jet rates and event shapes at LEP 1 and 2. More... | |
| class | ALICE_2010_S8624100 |
| class | ALICE_2010_S8625980 |
| class | ALICE_2010_S8706239 |
| class | ATLAS_2010_CONF_2010_049 |
| class | ATLAS_2010_S8591806 |
| ATLAS minimum bias analysis at 900 GeV. More... | |
| class | ATLAS_2010_S8817804 |
| ATLAS inclusive jet pT spectrum, di-jet Mass and di-jet chi. More... | |
| class | ATLAS_2010_S8894728 |
| class | ATLAS_2010_S8914702 |
| class | ATLAS_2010_S8918562 |
| Rivet analysis class for ATLAS_2010_S8918562 dataset. More... | |
| class | ATLAS_2010_S8919674 |
| class | ATLAS_2011_CONF_2011_090 |
| class | ATLAS_2011_S8924791 |
| ATLAS jet shape analysis. More... | |
| class | ATLAS_2011_S8971293 |
| class | ATLAS_2011_S8983313 |
| class | ATLAS_2011_S8994773 |
| class | ATLAS_2011_S9002537 |
| class | ATLAS_2011_S9019561 |
| class | ATLAS_2011_S9120807 |
| Measurement of isolated diphoton + X differential cross-sections. More... | |
| class | BELLE_2006_S6265367 |
| BELLE charmed mesons and baryons from fragmentation. More... | |
| class | CDF_1988_S1865951 |
CDF track 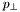 distributions at 630 and 1800 GeV. More... distributions at 630 and 1800 GeV. More... | |
| class | CDF_1990_S2089246 |
| CDF pseudorapidity analysis at 630 and 1800 GeV. More... | |
| class | CDF_1993_S2742446 |
| CDF <what is this analysis doing?> More... | |
| class | CDF_1994_S2952106 |
| CDF Run I color coherence analysis. More... | |
| class | CDF_1996_S3108457 |
| CDF properties of high-mass multi-jet events. More... | |
| class | CDF_1996_S3349578 |
| CDF properties of high-mass multi-jet events. More... | |
| class | CDF_1996_S3418421 |
| CDF dijet angular distributions. More... | |
| class | CDF_1997_S3541940 |
| CDF properties of 6-jet events with large 6-jet mass. More... | |
| class | CDF_1998_S3618439 |
| CDF diff cross-section in events with large missing energy. More... | |
| class | CDF_2000_S4155203 |
CDF Run I Z 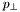 in Drell-Yan events. More... in Drell-Yan events. More... | |
| class | CDF_2000_S4266730 |
| CDF dijet cross-section, differential in dijet mass. More... | |
| class | CDF_2001_S4517016 |
| CDF two jet tripply-differential cross-section. More... | |
| class | CDF_2001_S4563131 |
| CDF Run I inclusive jet cross-section. More... | |
| class | CDF_2001_S4751469 |
| class | CDF_2002_S4796047 |
| class | CDF_2004_S5839831 |
| CDF calo jet underlying event analysis at 630 and 1800 GeV. More... | |
| class | CDF_2005_S6080774 |
| CDF diff cross-sections for prompt di-photon production. More... | |
| class | CDF_2005_S6217184 |
| CDF Run II jet shape analysis. More... | |
| class | CDF_2006_S6450792 |
CDF Inclusive jet cross-section differential in 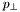 . More... . More... | |
| class | CDF_2006_S6653332 |
| class | CDF_2007_S7057202 |
CDF inclusive jet cross-section using the 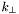 algorithm. More... algorithm. More... | |
| class | CDF_2008_LEADINGJETS |
| CDF Run II underlying event in leading jet events. More... | |
| class | CDF_2008_NOTE_9351 |
| CDF Run II underlying event in Drell-Yan. More... | |
| class | CDF_2008_S7540469 |
Measurement differential Z/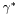 + jet + + jet + 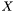 cross sections. More... cross sections. More... | |
| class | CDF_2008_S7541902 |
| CDF jet pT and multiplicity distributions in W + jets events. More... | |
| class | CDF_2008_S7782535 |
| CDF Run II b-jet shape paper. More... | |
| class | CDF_2008_S7828950 |
| CDF Run II inclusive jet cross-section using the Midpoint algorithm. More... | |
| class | CDF_2008_S8093652 |
| CDF dijet mass spectrum. More... | |
| class | CDF_2008_S8095620 |
| CDF Run II Z + b-jet cross-section measurement. More... | |
| class | CDF_2009_NOTE_9936 |
| class | CDF_2009_S8057893 |
| CDF in-jet kT distribution analysis. More... | |
| class | CDF_2009_S8233977 |
| class | CDF_2009_S8383952 |
| CDF Z boson rapidity measurement. More... | |
| class | CDF_2009_S8436959 |
| CDF inclusive isolated prompt photon cross-section. More... | |
| class | CDF_2010_S8591881_DY |
| CDF Run II underlying event in Drell-Yan. More... | |
| class | CDF_2010_S8591881_QCD |
| CDF Run II underlying event in leading jet events. More... | |
| class | CMS_2010_S8547297 |
| class | CMS_2010_S8656010 |
| class | CMS_2011_S8884919 |
| class | CMS_2011_S8957746 |
| Rivet analysis class for CMS_2011_S8957746 dataset. More... | |
| class | CMS_2011_S8968497 |
| class | CMS_2011_S8978280 |
| CMS strange particle spectra (Ks, Lambda, Cascade) in pp at 900 and 7000 GeV. More... | |
| class | D0_1996_S3214044 |
| D0 topological distributions of 3- and 4-jet events. More... | |
| class | D0_1996_S3324664 |
| D0 azimuthal correlation of jets widely separated in rapidity. More... | |
| class | D0_2000_S4480767 |
| class | D0_2001_S4674421 |
| D0 Run I differential W/Z boson cross-section analysis. More... | |
| class | D0_2004_S5992206 |
| class | D0_2006_S6438750 |
D0 inclusive isolated photon cross-section vs. 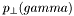 . More... . More... | |
| class | D0_2007_S7075677 |
Measurement of D0 Run II Z 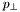 diff cross-section shape. More... diff cross-section shape. More... | |
| class | D0_2008_S6879055 |
D0 measurement of the ratio 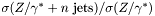 . More... . More... | |
| class | D0_2008_S7554427 |
D0 Run II Z 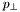 differential cross-section shape. More... differential cross-section shape. More... | |
| class | D0_2008_S7662670 |
| D0 differential jet cross sections. More... | |
| class | D0_2008_S7719523 |
| Measurement of isolated gamma + jet + X differential cross-sections. More... | |
| class | D0_2008_S7837160 |
| D0 Run II measurement of W charge asymmetry. More... | |
| class | D0_2008_S7863608 |
D0 differential Z/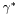 + jet + + jet + 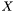 cross sections. More... cross sections. More... | |
| class | D0_2009_S8202443 |
D0 Z + jet + 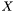 cross-section / cross-section / 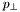 distributions. More... distributions. More... | |
| class | D0_2009_S8320160 |
| D0 dijet angular distributions. More... | |
| class | D0_2009_S8349509 |
| D0 Z+jets angular distributions. More... | |
| class | D0_2010_S8566488 |
| D0 dijet invariant mass measurement. More... | |
| class | D0_2010_S8570965 |
| D0 direct photon pair production. More... | |
| class | D0_2010_S8671338 |
| Measurement of Z(->muon muon) pT differential cross-section. More... | |
| class | D0_2010_S8821313 |
| class | DELPHI_1995_S3137023 |
| DELPHI strange baryon paper. More... | |
| class | DELPHI_1996_S3430090 |
| DELPHI event shapes and identified particle spectra. More... | |
| class | DELPHI_2002_069_CONF_603 |
| DELPHI b-fragmentation measurement. More... | |
| class | DELPHI_2003_WUD_03_11 |
| DELPHI 4-jet angular distributions. More... | |
| class | E735_1998_S3905616 |
| E735 charged multiplicity in NSD-triggered events. More... | |
| class | ExampleAnalysis |
| Just measures a few random things as an example. More... | |
| class | H1_1994_S2919893 |
| H1 energy flow and charged particle spectra. More... | |
| class | H1_1995_S3167097 |
| H1 energy flow in DIS. More... | |
| class | H1_2000_S4129130 |
| H1 energy flow and charged particle spectra. More... | |
| class | JADE_1998_S3612880 |
| class | JADE_OPAL_2000_S4300807 |
Jet rates in  at OPAL and JADE. More... at OPAL and JADE. More... | |
| class | LHCB_2010_S8758301 |
| class | MC_DIJET |
| MC validation analysis for di-jet events. More... | |
| class | MC_DIPHOTON |
| MC validation analysis for isolated di-photon events. More... | |
| class | MC_GENERIC |
| Generic analysis looking at various distributions of final state particles. More... | |
| class | MC_HJETS |
| MC validation analysis for higgs [-> tau tau] + jets events. More... | |
| class | MC_JETS |
| MC validation analysis for jet events. More... | |
| class | MC_LEADINGJETS |
| MC validation analysis for underlying event in jet events. More... | |
| class | MC_PHOTONJETS |
| MC validation analysis for photon + jets events. More... | |
| class | MC_PHOTONJETUE |
| MC validation analysis for underlying event in jet + isolated photon events. More... | |
| class | MC_SUSY |
| MC validation analysis for SUSY events. More... | |
| class | MC_TTBAR |
| class | MC_WJETS |
| MC validation analysis for W + jets events. More... | |
| class | MC_WPOL |
| MC validation analysis for W polarisation. More... | |
| class | MC_WWJETS |
| MC validation analysis for W^+[enu]W^-[munu] + jets events. More... | |
| class | MC_XS |
| Analysis for the generated cross section. More... | |
| class | MC_ZJETS |
| MC validation analysis for Z + jets events. More... | |
| class | MC_ZZJETS |
| MC validation analysis for Z[ee]Z[mumu] + jets events. More... | |
| class | OPAL_1993_S2692198 |
| OPAL photon production. More... | |
| class | OPAL_1998_S3780481 |
| OPAL flavour-dependent fragmentation paper. More... | |
| class | OPAL_2001_S4553896 |
| class | OPAL_2004_S6132243 |
| OPAL event shapes and moments at 91, 133, 177, and 197 GeV. More... | |
| class | PDG_HADRON_MULTIPLICITIES |
| Implementation of PDG hadron multiplicities. More... | |
| class | PDG_HADRON_MULTIPLICITIES_RATIOS |
Implementation of PDG hadron multiplicities as ratios to 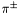 multiplicity. More... multiplicity. More... | |
| class | SFM_1984_S1178091 |
| SFM charged multiplicities in NSD and inelastic minbias events. More... | |
| class | STAR_2006_S6500200 |
| STAR identified hadron spectra in pp at 200 GeV. More... | |
| class | STAR_2006_S6860818 |
| STAR strange particle spectra in pp at 200 GeV. More... | |
| class | STAR_2006_S6870392 |
| STAR inclusive jet cross-section in pp at 200 GeV. More... | |
| class | STARRandomFilter |
| class | STAR_2008_S7869363 |
| class | STAR_2008_S7993412 |
| STAR di-hadron correlations in d-Au at 200 GeV. More... | |
| class | STAR_2009_UE_HELEN |
| STAR underlying event. More... | |
| class | TASSO_1990_S2148048 |
| class | UA1_1990_S2044935 |
UA1 minbias track multiplicities, 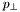 and and 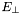 . More... . More... | |
| class | UA5_1982_S875503 |
UA5 multiplicity and 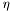 distributions. More... distributions. More... | |
| class | UA5_1986_S1583476 |
UA5 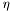 distributions at 200 and 900 GeV. More... distributions at 200 and 900 GeV. More... | |
| class | UA5_1987_S1640666 |
| class | UA5_1988_S1867512 |
| UA5 charged particle correlations at 200, 546 and 900 GeV. More... | |
| class | UA5_1989_S1926373 |
UA5 min bias charged multiplicities in central 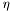 ranges. More... ranges. More... | |
| class | ZEUS_2001_S4815815 |
| ZEUS dijet photoproduction study used in the ZEUS Jets PDF fit. More... | |
Typedefs | |
| typedef Analysis * | AnalysisPtr |
| Smart (shared) pointer for handling projections. | |
| typedef shared_ptr< Analysis > | AnaHandle |
| Typedef for Analysis (smart) pointer. | |
| typedef Cmp< Projection > | PCmp |
| Typedef for Cmp<Projection> | |
| typedef Error | Exception |
| Rivet::Exception is a synonym for Rivet::Error. | |
| typedef std::map< HistoFormat, std::string > | HistoFormatMap |
| Typedef for a map of histogram format enums to strings. | |
| typedef std::map< std::string, HistoFormat > | HistoFormatMapR |
| Typedef for a map of histogram format name strings to enums. | |
| typedef std::vector< HistoFormat > | HistoFormatList |
| Typedef for a collection of histogram format name enums. | |
| typedef std::vector< Jet > | Jets |
| Typedef for a collection of Jet objects. | |
| typedef Matrix< 4 > | Matrix4 |
| typedef Vector3 | ThreeVector |
| typedef FourVector | Vector4 |
| typedef Projection * | ProjectionPtr |
| typedef const Projection * | ConstProjectionPtr |
| typedef shared_ptr< const Projection > | ProjHandle |
| Typedef for Projection (smart) pointer. | |
| typedef vector < fastjet::PseudoJet > | PseudoJets |
| Typedef for a collection of PseudoJets. | |
| typedef IsolationProjection < JetAlg, JetAlg > | AllJetsIso |
| typedef IsolationProjection < FinalState, FinalState > | AllParticleIso |
| typedef IsolationProjection < FinalState, JetAlg > | ParticleFromJetIso |
| typedef std::vector< double > | BinEdges |
| Typedef for a collection of bin edges. | |
| typedef boost::minstd_rand | RngBase |
| typedef boost::uniform_real | UniformRealDist |
| typedef boost::variate_generator < RngBase &, UniformRealDist > | UniformRealRNG |
| typedef boost::uniform_int | UniformIntDist |
| typedef boost::variate_generator < RngBase &, UniformIntDist > | UniformIntRNG |
| typedef std::pair< double, double > | doublepair |
Particle declarations | |
| typedef std::vector< Particle > | ParticleVector |
| Typedef for a vector of Particle objects. | |
| typedef std::pair< Particle, Particle > | ParticlePair |
| Typedef for a pair of Particle objects. | |
PdgId declarations | |
| typedef int | PdgId |
| Typedef for a PDG ID code. | |
| typedef std::pair< PdgId, PdgId > | PdgIdPair |
| Typedef for a pair of particle names. | |
Enumerations | |
| enum | CmpState { UNDEFINED = -2, ASC = -1, ORDERED = -1, EQUIVALENT = 0, DESC = 1, UNORDERED = 1, ANTIORDERED = 1 } |
Enumerate the possible states of a Cmp object. More... | |
| enum | HistoFormat { AIDAML, FLAT, ROOT } |
Enumeration of available histogram output formats. More... | |
| enum | Sign { MINUS = -1, ZERO = 0, PLUS = 1 } |
Enum for signs of numbers. More... | |
| enum | RapScheme { PSEUDORAPIDITY = 0, ETA = 0, RAPIDITY = 1, YRAP = 1 } |
Enum for rapidity variable to be used in calculating | |
| enum | PhiMapping { MINUSPI_PLUSPI, ZERO_2PI } |
Enum for range of | |
Functions | |
| std::string | toString (const AnalysisInfo &ai) |
| String representation. | |
| std::ostream & | operator<< (std::ostream &os, const AnalysisInfo &ai) |
| Stream an AnalysisInfo as a text description. | |
| bool | compatible (PdgId p, PdgId allowed) |
| bool | compatible (const PdgIdPair &pair, const PdgIdPair &allowedpair) |
| bool | compatible (const ParticlePair &ppair, const PdgIdPair &allowedpair) |
| Check particle compatibility of Particle pairs. | |
| bool | compatible (const PdgIdPair &allowedpair, const ParticlePair &ppair) |
| Check particle compatibility of Particle pairs (for symmetric completeness). | |
| bool | compatible (const PdgIdPair &pair, const set< PdgIdPair > &allowedpairs) |
| set< PdgIdPair > | intersection (const set< PdgIdPair > &a, const set< PdgIdPair > &b) |
| Return the intersection of two sets of {PdgIdPair}s. | |
| template<typename T > | |
| Cmp< T > | cmp (const T &t1, const T &t2) |
| Global helper function for easy creation of Cmp objects. | |
| Cmp< Projection > | pcmp (const Projection &p1, const Projection &p2) |
| Global helper function for easy creation of Cmp<Projection> objects. | |
| Cmp< Projection > | pcmp (const Projection &parent1, const Projection &parent2, const string &pname) |
| Cmp< Projection > | pcmp (const Projection *parent1, const Projection &parent2, const string &pname) |
| Cmp< Projection > | pcmp (const Projection &parent1, const Projection *parent2, const string &pname) |
| Cmp< Projection > | pcmp (const Projection *parent1, const Projection *parent2, const string &pname) |
| HistoFormatMap | getKnownHistoFormats () |
| Function which returns a map from histogram format enums to the corresponding name strings. | |
| HistoFormatMapR | getKnownHistoFormatsR () |
| Function which returns a map from histogram format name strings to the corresponding enums. | |
| HistoFormatList | getKnownHistoFormatEnums () |
| std::vector< std::string > | getKnownHistoFormatNames () |
| Function which returns a vector of all the histogram format name strings. | |
| double | deltaR (const Jet &j1, const Jet &j2, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Jet &j, const Particle &p, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Particle &p, const Jet &j, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Jet &j, const FourMomentum &v, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Jet &j, const FourVector &v, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Jet &j, const Vector3 &v) |
| double | deltaR (const Jet &j, double eta, double phi) |
| double | deltaR (const FourMomentum &v, const Jet &j, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const FourVector &v, const Jet &j, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Vector3 &v, const Jet &j) |
| double | deltaR (double eta, double phi, const Jet &j) |
| double | deltaPhi (const Jet &j1, const Jet &j2) |
| double | deltaPhi (const Jet &j, const Particle &p) |
| double | deltaPhi (const Particle &p, const Jet &j) |
| double | deltaPhi (const Jet &j, const FourMomentum &v) |
| double | deltaPhi (const Jet &j, const FourVector &v) |
| double | deltaPhi (const Jet &j, const Vector3 &v) |
| double | deltaPhi (const Jet &j, double phi) |
| double | deltaPhi (const FourMomentum &v, const Jet &j) |
| double | deltaPhi (const FourVector &v, const Jet &j) |
| double | deltaPhi (const Vector3 &v, const Jet &j) |
| double | deltaPhi (double phi, const Jet &j) |
| double | deltaEta (const Jet &j1, const Jet &j2) |
| double | deltaEta (const Jet &j, const Particle &p) |
| double | deltaEta (const Particle &p, const Jet &j) |
| double | deltaEta (const Jet &j, const FourMomentum &v) |
| double | deltaEta (const Jet &j, const FourVector &v) |
| double | deltaEta (const Jet &j, const Vector3 &v) |
| double | deltaEta (const Jet &j, double eta) |
| double | deltaEta (const FourMomentum &v, const Jet &j) |
| double | deltaEta (const FourVector &v, const Jet &j) |
| double | deltaEta (const Vector3 &v, const Jet &j) |
| double | deltaEta (double eta, const Jet &j) |
| double | lorentzGamma (const double beta) |
| LorentzTransform | inverse (const LorentzTransform <) |
| LorentzTransform | combine (const LorentzTransform &a, const LorentzTransform &b) |
| FourVector | transform (const LorentzTransform <, const FourVector &v4) |
| string | toString (const LorentzTransform <) |
| ostream & | operator<< (std::ostream &out, const LorentzTransform <) |
| template<size_t N> | |
| EigenSystem< N > | diagonalize (const Matrix< N > &m) |
| template<size_t N> | |
| const string | toString (const typename EigenSystem< N >::EigenPair &e) |
| template<size_t N> | |
| ostream & | operator<< (std::ostream &out, const typename EigenSystem< N >::EigenPair &e) |
| template<size_t N> | |
| Matrix< N > | multiply (const Matrix< N > &a, const Matrix< N > &b) |
| template<size_t N> | |
| Matrix< N > | divide (const Matrix< N > &, const double) |
| template<size_t N> | |
| Matrix< N > | operator* (const Matrix< N > &a, const Matrix< N > &b) |
| template<size_t N> | |
| Matrix< N > | add (const Matrix< N > &a, const Matrix< N > &b) |
| template<size_t N> | |
| Matrix< N > | subtract (const Matrix< N > &a, const Matrix< N > &b) |
| template<size_t N> | |
| Matrix< N > | operator+ (const Matrix< N > a, const Matrix< N > &b) |
| template<size_t N> | |
| Matrix< N > | operator- (const Matrix< N > a, const Matrix< N > &b) |
| template<size_t N> | |
| Matrix< N > | multiply (const double a, const Matrix< N > &m) |
| template<size_t N> | |
| Matrix< N > | multiply (const Matrix< N > &m, const double a) |
| template<size_t N> | |
| Matrix< N > | operator* (const double a, const Matrix< N > &m) |
| template<size_t N> | |
| Matrix< N > | operator* (const Matrix< N > &m, const double a) |
| template<size_t N> | |
| Vector< N > | multiply (const Matrix< N > &a, const Vector< N > &b) |
| template<size_t N> | |
| Vector< N > | operator* (const Matrix< N > &a, const Vector< N > &b) |
| template<size_t N> | |
| Matrix< N > | transpose (const Matrix< N > &m) |
| template<size_t N> | |
| Matrix< N > | inverse (const Matrix< N > &m) |
| template<size_t N> | |
| double | det (const Matrix< N > &m) |
| template<size_t N> | |
| double | trace (const Matrix< N > &m) |
| template<size_t N> | |
| string | toString (const Matrix< N > &m) |
| Make string representation. | |
| template<size_t N> | |
| ostream & | operator<< (std::ostream &out, const Matrix< N > &m) |
| Stream out string representation. | |
| template<size_t N> | |
| bool | fuzzyEquals (const Matrix< N > &ma, const Matrix< N > &mb, double tolerance=1E-5) |
| Compare two matrices by index, allowing for numerical precision. | |
| template<size_t N> | |
| bool | isZero (const Matrix< N > &m, double tolerance=1E-5) |
| External form of numerically safe nullness check. | |
| Vector3 | multiply (const double, const Vector3 &) |
| Vector3 | multiply (const Vector3 &, const double) |
| Vector3 | add (const Vector3 &, const Vector3 &) |
| Vector3 | operator* (const double, const Vector3 &) |
| Vector3 | operator* (const Vector3 &, const double) |
| Vector3 | operator/ (const Vector3 &, const double) |
| Vector3 | operator+ (const Vector3 &, const Vector3 &) |
| Vector3 | operator- (const Vector3 &, const Vector3 &) |
| double | dot (const Vector3 &a, const Vector3 &b) |
| Vector3 | cross (const Vector3 &a, const Vector3 &b) |
| Vector3 | subtract (const Vector3 &a, const Vector3 &b) |
| double | angle (const Vector3 &a, const Vector3 &b) |
| Angle (in radians) between two 3-vectors. | |
| double | polarRadius2 (const Vector3 &v) |
Calculate transverse length sq. 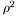 of a 3-vector. of a 3-vector. | |
| double | perp2 (const Vector3 &v) |
| Synonym for polarRadius2. | |
| double | rho2 (const Vector3 &v) |
| Synonym for polarRadius2. | |
| double | polarRadius (const Vector3 &v) |
Calculate transverse length 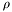 of a 3-vector. of a 3-vector. | |
| double | perp (const Vector3 &v) |
| Synonym for polarRadius. | |
| double | rho (const Vector3 &v) |
| Synonym for polarRadius. | |
| double | azimuthalAngle (const Vector3 &v, const PhiMapping mapping=ZERO_2PI) |
| Calculate azimuthal angle of a 3-vector. Returns a number in (-pi, pi] or in [0, 2pi) according to the mapping scheme selected. | |
| double | phi (const Vector3 &v, const PhiMapping mapping=ZERO_2PI) |
| Synonym for azimuthalAngle. | |
| double | polarAngle (const Vector3 &v) |
| Calculate polar angle of a 3-vector. | |
| double | theta (const Vector3 &v) |
| Synonym for polarAngle. | |
| double | pseudorapidity (const Vector3 &v) |
| Calculate pseudorapidity of a 3-vector. | |
| double | eta (const Vector3 &v) |
| Synonym for pseudorapidity. | |
| double | contract (const FourVector &a, const FourVector &b) |
| Contract two 4-vectors, with metric signature (+ - - -). | |
| double | dot (const FourVector &a, const FourVector &b) |
| Contract two 4-vectors, with metric signature (+ - - -). | |
| FourVector | multiply (const double a, const FourVector &v) |
| FourVector | multiply (const FourVector &v, const double a) |
| FourVector | operator* (const double a, const FourVector &v) |
| FourVector | operator* (const FourVector &v, const double a) |
| FourVector | operator/ (const FourVector &v, const double a) |
| FourVector | add (const FourVector &a, const FourVector &b) |
| FourVector | operator+ (const FourVector &a, const FourVector &b) |
| FourVector | operator- (const FourVector &a, const FourVector &b) |
| double | invariant (const FourVector &lv) |
| double | angle (const FourVector &a, const FourVector &b) |
| Angle (in radians) between spatial parts of two Lorentz vectors. | |
| double | angle (const Vector3 &a, const FourVector &b) |
| Angle (in radians) between spatial parts of two Lorentz vectors. | |
| double | angle (const FourVector &a, const Vector3 &b) |
| Angle (in radians) between spatial parts of two Lorentz vectors. | |
| double | polarRadius2 (const FourVector &v) |
Calculate transverse length sq. 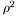 of a Lorentz vector. of a Lorentz vector. | |
| double | perp2 (const FourVector &v) |
| Synonym for polarRadius2. | |
| double | rho2 (const FourVector &v) |
| Synonym for polarRadius2. | |
| double | polarRadius (const FourVector &v) |
Calculate transverse length 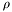 of a Lorentz vector. of a Lorentz vector. | |
| double | perp (const FourVector &v) |
| Synonym for polarRadius. | |
| double | rho (const FourVector &v) |
| Synonym for polarRadius. | |
| double | azimuthalAngle (const FourVector &v, const PhiMapping mapping=ZERO_2PI) |
| Calculate azimuthal angle of a Lorentz vector. | |
| double | phi (const FourVector &v, const PhiMapping mapping=ZERO_2PI) |
| Synonym for azimuthalAngle. | |
| double | polarAngle (const FourVector &v) |
| Calculate polar angle of a Lorentz vector. | |
| double | theta (const FourVector &v) |
| Synonym for polarAngle. | |
| double | pseudorapidity (const FourVector &v) |
| Calculate pseudorapidity of a Lorentz vector. | |
| double | eta (const FourVector &v) |
| Synonym for pseudorapidity. | |
| FourMomentum | multiply (const double a, const FourMomentum &v) |
| FourMomentum | multiply (const FourMomentum &v, const double a) |
| FourMomentum | operator* (const double a, const FourMomentum &v) |
| FourMomentum | operator* (const FourMomentum &v, const double a) |
| FourMomentum | operator/ (const FourMomentum &v, const double a) |
| FourMomentum | add (const FourMomentum &a, const FourMomentum &b) |
| FourMomentum | operator+ (const FourMomentum &a, const FourMomentum &b) |
| FourMomentum | operator- (const FourMomentum &a, const FourMomentum &b) |
| double | mass (const FourMomentum &v) |
Get the mass 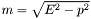 (the Lorentz self-invariant) of a momentum 4-vector. (the Lorentz self-invariant) of a momentum 4-vector. | |
| double | massT (const FourMomentum &v) |
Get the transverse mass 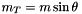 of a momentum 4-vector. of a momentum 4-vector. | |
| double | mass2 (const FourMomentum &v) |
Get the squared mass  (the Lorentz self-invariant) of a momentum 4-vector. (the Lorentz self-invariant) of a momentum 4-vector. | |
| double | massT2 (const FourMomentum &v) |
Get the squared transverse mass 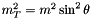 of a momentum 4-vector. of a momentum 4-vector. | |
| double | rapidity (const FourMomentum &v) |
| Calculate the rapidity of a momentum 4-vector. | |
| double | pT2 (const FourMomentum &v) |
Calculate the squared transverse momentum 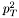 of a momentum 4-vector. of a momentum 4-vector. | |
| double | pT (const FourMomentum &v) |
Calculate the transverse momentum 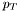 of a momentum 4-vector. of a momentum 4-vector. | |
| double | Et2 (const FourMomentum &v) |
Calculate the transverse energy squared, 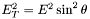 of a momentum 4-vector. of a momentum 4-vector. | |
| double | Et (const FourMomentum &v) |
Calculate the transverse energy 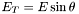 of a momentum 4-vector. of a momentum 4-vector. | |
| Vector3 | boostVector (const FourMomentum &v) |
| Calculate the velocity boost vector of a momentum 4-vector. | |
| template<size_t N> | |
| double | mod2 (const Vector< N > &v) |
| template<size_t N> | |
| double | mod (const Vector< N > &v) |
| template<size_t N> | |
| bool | fuzzyEquals (const Vector< N > &va, const Vector< N > &vb, double tolerance=1E-5) |
| Compare two vectors by index, allowing for numerical precision. | |
| template<size_t N> | |
| bool | isZero (const Vector< N > &v, double tolerance=1E-5) |
| External form of numerically safe nullness check. | |
| double | deltaR (const Particle &p1, const Particle &p2, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Particle &p, const FourMomentum &v, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Particle &p, const FourVector &v, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Particle &p, const Vector3 &v) |
| double | deltaR (const Particle &p, double eta, double phi) |
| double | deltaR (const FourMomentum &v, const Particle &p, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const FourVector &v, const Particle &p, RapScheme scheme=PSEUDORAPIDITY) |
| double | deltaR (const Vector3 &v, const Particle &p) |
| double | deltaR (double eta, double phi, const Particle &p) |
| double | deltaPhi (const Particle &p1, const Particle &p2) |
| double | deltaPhi (const Particle &p, const FourMomentum &v) |
| double | deltaPhi (const Particle &p, const FourVector &v) |
| double | deltaPhi (const Particle &p, const Vector3 &v) |
| double | deltaPhi (const Particle &p, double phi) |
| double | deltaPhi (const FourMomentum &v, const Particle &p) |
| double | deltaPhi (const FourVector &v, const Particle &p) |
| double | deltaPhi (const Vector3 &v, const Particle &p) |
| double | deltaPhi (double phi, const Particle &p) |
| double | deltaEta (const Particle &p1, const Particle &p2) |
| double | deltaEta (const Particle &p, const FourMomentum &v) |
| double | deltaEta (const Particle &p, const FourVector &v) |
| double | deltaEta (const Particle &p, const Vector3 &v) |
| double | deltaEta (const Particle &p, double eta) |
| double | deltaEta (const FourMomentum &v, const Particle &p) |
| double | deltaEta (const FourVector &v, const Particle &p) |
| double | deltaEta (const Vector3 &v, const Particle &p) |
| double | deltaEta (double eta, const Particle &p) |
| const std::string & | toParticleName (PdgId p) |
| Print a PdgId as a named string. | |
| PdgId | toParticleId (const std::string &pname) |
| Print a PdgId as a named string. | |
| std::pair< PdgId, PdgId > | make_pdgid_pair (PdgId a, PdgId b) |
| Convenience maker of particle ID pairs from PdgIds. | |
| std::pair< PdgId, PdgId > | make_pdgid_pair (const std::string &a, const std::string &b) |
| Convenience maker of particle ID pairs from particle names. | |
| std::string | toBeamsString (const PdgIdPair &pair) |
| Print a PdgIdPair as a string. | |
| template<typename PROJ > | |
| const PROJ & | pcast (const Projection &p) |
| Convenience method for casting to a const Projection reference. | |
| template<typename PROJ > | |
| const PROJ * | pcast (const Projection *p) |
| Convenience method for casting to a const Projection pointer. | |
| Vector3 | momentum3 (const fastjet::PseudoJet &pj) |
| Make a 3-momentum vector from a FastJet pseudo-jet. | |
| FourMomentum | momentum (const fastjet::PseudoJet &pj) |
| Make a 4-momentum vector from a FastJet pseudo-jet. | |
| bool | cmpMomByPt (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscPt (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByP (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscP (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByEt (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscEt (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByE (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscE (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByDescPseudorapidity (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscPseudorapidity (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByDescAbsPseudorapidity (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscAbsPseudorapidity (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByDescRapidity (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscRapidity (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByDescAbsRapidity (const FourMomentum &a, const FourMomentum &b) |
| bool | cmpMomByAscAbsRapidity (const FourMomentum &a, const FourMomentum &b) |
| string | version () |
| A function to get the Rivet version string. | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &os, const std::vector< T > &vec) |
| Convenient function for streaming out vectors of any streamable object. | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &os, const std::list< T > &vec) |
| Convenient function for streaming out lists of any streamable object. | |
| AIDA::IAnalysisFactory * | createAnalysisFactory () |
| Get an AIDA system (LWH impl.). | |
| map< string, BinEdges > | getBinEdges (string papername) |
| map< string, BinEdges > | getBinEdges (const map< string, vector< DPSXPoint > > &xpoints) |
| map< string, vector< DPSXPoint > > | getDPSXValsErrs (string papername) |
| map< string, vector< DPSXYPoint > > | getDPSXYValsErrs (string papername) |
| string | getDatafilePath (string papername) |
| Get the file system path to the AIDA reference file for this paper. | |
| double | integral (AIDA::IHistogram1D *histo) |
| Return the integral over the histogram bins. | |
| vector< GenParticle * > | particles (const GenEvent &ge) |
| vector< GenParticle * > | particles (const GenEvent *ge) |
| vector< GenVertex * > | vertices (const GenEvent &ge) |
| vector< GenVertex * > | vertices (const GenEvent *ge) |
| const std::pair < GenVertex::particles_in_const_iterator, GenVertex::particles_in_const_iterator > | particles_in (const GenVertex *gv) |
| const std::pair < GenVertex::particles_out_const_iterator, GenVertex::particles_out_const_iterator > | particles_out (const GenVertex *gv) |
| vector< GenParticle * > | particles (GenVertex *gv, HepMC::IteratorRange range=HepMC::relatives) |
| std::ostream & | operator<< (Log &log, int level) |
| Streaming output to a logger must have a Log::Level/int as its first argument. | |
| int | nocase_cmp (const string &s1, const string &s2) |
| string | toLower (const string &s) |
| string | toUpper (const string &s) |
| bool | startsWith (const string &s, const string &start) |
| bool | endsWith (const string &s, const string &end) |
| Check whether a string end is found at the end of s. | |
| vector< string > | pathsplit (const string &path) |
| Split a path string with colon delimiters. Ignores zero-length substrings. Designed for getting elements of filesystem paths, naturally. | |
| vector< string > | split (const string &path, const string &UNUSED(delim)=":") |
| string | pathjoin (const vector< string > &paths) |
Join several filesystem paths together with a delimiter character. Note that this does NOT join path elements together with a platform-portable directory delimiter, cf. the Python {os.path.join}! | |
| void | _geRot180x (GenEvent &ge) |
| bool | chargedParticleFilter (const Particle &p) |
| bool | hadronFilter (const Particle &p) |
| bool | mod2Cmp (const Vector< 2 > &a, const Vector< 2 > &b) |
| double | dot (const Vector< 2 > &a, const Vector< 2 > &b) |
| Vector< 2 > | unit (const Vector< 2 > &v) |
| void | _calcS (const vector< Vector3 > &perpmomenta, double &sphero, Vector3 &saxis) |
| double | get2dClosestApproach (const HepMC::GenParticle &track, const Vector3 &vtx3pos) |
| double | get3dClosestApproach (const HepMC::GenParticle &track, const Vector3 &vtx3pos) |
| double | get2dDecayLength (const Vector3 &vtx1, const Vector3 &vtx2, const FourMomentum &jetaxis) |
| Return Decay Length Significance between two vertices in transverse plane. | |
| double | get3dDecayLength (const Vector3 &vtx1, const Vector3 &vtx2, const FourMomentum &jetaxis) |
| Return 3 dimensional Decay Length Significance between vertices. | |
| bool | mod2Cmp (const Vector3 &a, const Vector3 &b) |
| void | _calcT (const vector< Vector3 > &momenta, double &t, Vector3 &taxis) |
| void | _updateLevels (const Log::LevelMap &defaultLevels, Log::LogMap &existingLogs) |
| string | _findFile (const string &filename, const vector< string > &paths) |
Jet comparison functions for STL sorting | |
| bool | cmpJetsByPt (const Jet &a, const Jet &b) |
Compare jets by 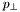 (descending - usual sorting for HEP) Use this so that highest (descending - usual sorting for HEP) Use this so that highest 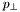 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByAscPt (const Jet &a, const Jet &b) |
Compare jets by 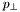 (ascending) Use this so that lowest (ascending) Use this so that lowest 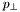 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByP (const Jet &a, const Jet &b) |
Compare jets by descending momentum, 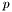 . . | |
| bool | cmpJetsByAscP (const Jet &a, const Jet &b) |
Compare jets by ascending momentum, 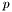 . . | |
| bool | cmpJetsByEt (const Jet &a, const Jet &b) |
Use this so that highest 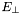 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByEtDesc (const Jet &a, const Jet &b) |
Use this so that lowest 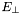 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByE (const Jet &a, const Jet &b) |
Compare jets by 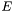 (descending - usual sorting for HEP) Use this so that highest (descending - usual sorting for HEP) Use this so that highest 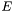 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByAscE (const Jet &a, const Jet &b) |
Compare jets by 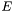 (ascending) Use this so that lowest (ascending) Use this so that lowest 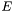 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByDescPseudorapidity (const Jet &a, const Jet &b) |
Compare jets by 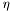 (descending) Use this so that highest (descending) Use this so that highest 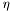 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByAscPseudorapidity (const Jet &a, const Jet &b) |
Compare jets by 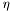 (ascending) Use this so that lowest (ascending) Use this so that lowest 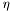 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByDescAbsPseudorapidity (const Jet &a, const Jet &b) |
Compare jets by 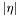 (descending) Use this so that highest (descending) Use this so that highest 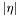 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByAscAbsPseudorapidity (const Jet &a, const Jet &b) |
Compare jets by 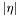 (ascending) Use this so that lowest (ascending) Use this so that lowest 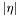 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByDescRapidity (const Jet &a, const Jet &b) |
Compare jets by 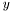 (descending) Use this so that highest (descending) Use this so that highest 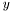 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByAscRapidity (const Jet &a, const Jet &b) |
Compare jets by 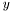 (ascending) Use this so that lowest (ascending) Use this so that lowest 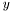 is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByDescAbsRapidity (const Jet &a, const Jet &b) |
Compare jets by  (descending) Use this so that highest (descending) Use this so that highest  is at the front of the list. is at the front of the list. | |
| bool | cmpJetsByAscAbsRapidity (const Jet &a, const Jet &b) |
Compare jets by  (ascending) Use this so that lowest (ascending) Use this so that lowest  is at the front of the list. is at the front of the list. | |
Comparison functions for safe floating point equality tests | |
| bool | isZero (double val, double tolerance=1E-8) |
| bool | isZero (long val, double UNUSED(tolerance)=1E-8) |
| bool | fuzzyEquals (double a, double b, double tolerance=1E-5) |
| Compare two floating point numbers for equality with a degree of fuzziness The tolerance parameter is fractional. | |
| bool | fuzzyEquals (long a, long b, double UNUSED(tolerance)=1E-5) |
Compare two integral-type numbers for equality with a degree of fuzziness. Since there is no risk of floating point error with integral types, this function just exists in case fuzzyEquals is accidentally used on an integer type, to avoid implicit type conversion. The tolerance parameter is ignored, even if it would have an absolute magnitude greater than 1. | |
| bool | fuzzyGtrEquals (double a, double b, double tolerance=1E-5) |
Compare two floating point numbers for >= with a degree of fuzziness The tolerance parameter on the equality test is as for fuzzyEquals. | |
| bool | fuzzyGtrEquals (long a, long b, double UNUSED(tolerance)=1E-5) |
Compare two integral-type numbers for >= with a degree of fuzziness. Since there is no risk of floating point error with integral types, this function just exists in case fuzzyGtrEquals is accidentally used on an integer type, to avoid implicit type conversion. The tolerance parameter is ignored, even if it would have an absolute magnitude greater than 1. | |
| bool | fuzzyLessEquals (double a, double b, double tolerance=1E-5) |
Compare two floating point numbers for <= with a degree of fuzziness The tolerance parameter on the equality test is as for fuzzyEquals. | |
| bool | fuzzyLessEquals (long a, long b, double UNUSED(tolerance)=1E-5) |
Compare two integral-type numbers for <= with a degree of fuzziness. Since there is no risk of floating point error with integral types, this function just exists in case fuzzyLessEquals is accidentally used on an integer type, to avoid implicit type conversion. The tolerance parameter is ignored, even if it would have an absolute magnitude greater than 1. | |
Miscellaneous numerical helpers | |
| template<typename NUM > | |
| NUM | sqr (NUM a) |
| Named number-type squaring operation. | |
| template<typename Num > | |
| Num | add_quad (Num a, Num b) |
| Named number-type addition in quadrature operation. | |
| template<typename Num > | |
| Num | add_quad (Num a, Num b, Num c) |
| Named number-type addition in quadrature operation. | |
| template<typename Num > | |
| Num | intpow (Num val, unsigned int exp) |
| A more efficient version of pow for raising numbers to integer powers. | |
| int | sign (double val) |
| Find the sign of a number. | |
| int | sign (int val) |
| Find the sign of a number. | |
| int | sign (long val) |
| Find the sign of a number. | |
Binning helper functions | |
| vector< double > | linspace (double start, double end, size_t nbins) |
| Make a list of nbins + 1 values equally spaced between start and end inclusive. | |
| vector< double > | logspace (double start, double end, size_t nbins) |
| Make a list of nbins + 1 values exponentially spaced between start and end inclusive. | |
| template<typename NUM > | |
| int | index_between (const NUM &val, const vector< NUM > &binedges) |
| Return the bin index of the given value, val, given a vector of bin edges NB. The binedges vector must be sorted. | |
Statistics functions | |
| double | mean (const vector< int > &sample) |
| Calculate the mean of a sample. | |
| double | mean_err (const vector< int > &sample) |
| double | covariance (const vector< int > &sample1, const vector< int > &sample2) |
| Calculate the covariance (variance) between two samples. | |
| double | covariance_err (const vector< int > &sample1, const vector< int > &sample2) |
| Calculate the error on the covariance (variance) of two samples, assuming poissonian errors. | |
| double | correlation (const vector< int > &sample1, const vector< int > &sample2) |
| Calculate the correlation strength between two samples. | |
| double | correlation_err (const vector< int > &sample1, const vector< int > &sample2) |
| Calculate the error of the correlation strength between two samples assuming Poissonian errors. | |
Angle range mappings | |
| double | _mapAngleM2PITo2Pi (double angle) |
| double | mapAngleMPiToPi (double angle) |
| Map an angle into the range (-PI, PI]. | |
| double | mapAngle0To2Pi (double angle) |
| Map an angle into the range [0, 2PI). | |
| double | mapAngle0ToPi (double angle) |
| Map an angle into the range [0, PI]. | |
Phase space measure helpers | |
| double | deltaPhi (double phi1, double phi2) |
| double | deltaEta (double eta1, double eta2) |
| double | deltaR (double rap1, double phi1, double rap2, double phi2) |
| double | rapidity (double E, double pz) |
| Calculate a rapidity value from the supplied energy E and longitudinal momentum pz. | |
\f$ |\Delta eta| \f$ calculations from 3-vectors | |
| double | deltaEta (const Vector3 &a, const Vector3 &b) |
| Calculate the difference in pseudorapidity between two spatial vectors. | |
| double | deltaEta (const Vector3 &v, double eta2) |
| Calculate the difference in pseudorapidity between two spatial vectors. | |
| double | deltaEta (double eta1, const Vector3 &v) |
| Calculate the difference in pseudorapidity between two spatial vectors. | |
\f$ \Delta phi \f$ calculations from 3-vectors | |
| double | deltaPhi (const Vector3 &a, const Vector3 &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const Vector3 &v, double phi2) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (double phi1, const Vector3 &v) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
\f$ \Delta R \f$ calculations from 3-vectors | |
| double | deltaR (const Vector3 &a, const Vector3 &b) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two spatial vectors. | |
| double | deltaR (const Vector3 &v, double eta2, double phi2) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two spatial vectors. | |
| double | deltaR (double eta1, double phi1, const Vector3 &v) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two spatial vectors. | |
\f$ \Delta R \f$ calculations from 4-vectors | |
| double | deltaR (const FourVector &a, const FourVector &b, RapScheme scheme=PSEUDORAPIDITY) |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. Use of this scheme option is discouraged in this case since RAPIDITY is only a valid option for vectors whose type is really the FourMomentum derived class. | |
| double | deltaR (const FourVector &v, double eta2, double phi2, RapScheme scheme=PSEUDORAPIDITY) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. | |
| double | deltaR (double eta1, double phi1, const FourVector &v, RapScheme scheme=PSEUDORAPIDITY) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. | |
| double | deltaR (const FourMomentum &a, const FourMomentum &b, RapScheme scheme=PSEUDORAPIDITY) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. | |
| double | deltaR (const FourMomentum &v, double eta2, double phi2, RapScheme scheme=PSEUDORAPIDITY) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. | |
| double | deltaR (double eta1, double phi1, const FourMomentum &v, RapScheme scheme=PSEUDORAPIDITY) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. | |
| double | deltaR (const FourMomentum &a, const FourVector &b, RapScheme scheme=PSEUDORAPIDITY) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. | |
| double | deltaR (const FourVector &a, const FourMomentum &b, RapScheme scheme=PSEUDORAPIDITY) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. | |
| double | deltaR (const FourMomentum &a, const Vector3 &b) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector. | |
| double | deltaR (const Vector3 &a, const FourMomentum &b) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector. | |
| double | deltaR (const FourVector &a, const Vector3 &b) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector. | |
| double | deltaR (const Vector3 &a, const FourVector &b) |
| Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector. | |
\f$ \Delta phi \f$ calculations from 4-vectors | |
| double | deltaPhi (const FourMomentum &a, const FourMomentum &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const FourMomentum &v, double phi2) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (double phi1, const FourMomentum &v) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const FourVector &a, const FourVector &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const FourVector &v, double phi2) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (double phi1, const FourVector &v) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const FourVector &a, const FourMomentum &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const FourMomentum &a, const FourVector &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const FourVector &a, const Vector3 &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const Vector3 &a, const FourVector &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const FourMomentum &a, const Vector3 &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaPhi (const Vector3 &a, const FourMomentum &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
\f$ |\Delta eta| \f$ calculations from 4-vectors | |
| double | deltaEta (const FourMomentum &a, const FourMomentum &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const FourMomentum &v, double eta2) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (double eta1, const FourMomentum &v) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const FourVector &a, const FourVector &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const FourVector &v, double eta2) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (double eta1, const FourVector &v) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const FourVector &a, const FourMomentum &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const FourMomentum &a, const FourVector &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const FourVector &a, const Vector3 &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const Vector3 &a, const FourVector &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const FourMomentum &a, const Vector3 &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
| double | deltaEta (const Vector3 &a, const FourMomentum &b) |
| Calculate the difference in azimuthal angle between two spatial vectors. | |
4-vector string representations | |
| const string | toString (const FourVector &lv) |
| Render a 4-vector as a string. | |
| std::ostream & | operator<< (std::ostream &out, const FourVector &lv) |
| Write a 4-vector to an ostream. | |
String representations of vectors | |
| template<size_t N> | |
| const string | toString (const Vector< N > &v) |
| Make string representation. | |
| template<size_t N> | |
| std::ostream & | operator<< (std::ostream &out, const Vector< N > &v) |
| Stream out string representation. | |
String representation | |
| std::string | toString (const ParticlePair &pair) |
| Print a ParticlePair as a string. | |
| std::ostream & | operator<< (std::ostream &os, const ParticlePair &pp) |
| Allow ParticlePair to be passed to an ostream. | |
Comparison functors | |
| bool | cmpParticleByPt (const Particle &a, const Particle &b) |
Sort by descending transverse momentum, 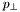 . . | |
| bool | cmpParticleByAscPt (const Particle &a, const Particle &b) |
Sort by ascending transverse momentum, 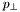 . . | |
| bool | cmpParticleByP (const Particle &a, const Particle &b) |
Sort by descending momentum, 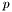 . . | |
| bool | cmpParticleByAscP (const Particle &a, const Particle &b) |
Sort by ascending momentum, 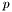 . . | |
| bool | cmpParticleByEt (const Particle &a, const Particle &b) |
Sort by descending transverse energy, 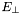 . . | |
| bool | cmpParticleByAscEt (const Particle &a, const Particle &b) |
Sort by ascending transverse energy, 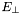 . . | |
| bool | cmpParticleByE (const Particle &a, const Particle &b) |
Sort by descending energy, 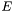 . . | |
| bool | cmpParticleByAscE (const Particle &a, const Particle &b) |
Sort by ascending energy, 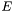 . . | |
| bool | cmpParticleByDescPseudorapidity (const Particle &a, const Particle &b) |
Sort by descending pseudorapidity, 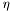 . . | |
| bool | cmpParticleByAscPseudorapidity (const Particle &a, const Particle &b) |
Sort by ascending pseudorapidity, 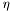 . . | |
| bool | cmpParticleByDescAbsPseudorapidity (const Particle &a, const Particle &b) |
Sort by descending absolute pseudorapidity, 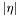 . . | |
| bool | cmpParticleByAscAbsPseudorapidity (const Particle &a, const Particle &b) |
Sort by ascending absolute pseudorapidity, 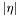 . . | |
| bool | cmpParticleByDescRapidity (const Particle &a, const Particle &b) |
Sort by descending rapidity, 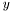 . . | |
| bool | cmpParticleByAscRapidity (const Particle &a, const Particle &b) |
Sort by ascending rapidity, 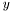 . . | |
| bool | cmpParticleByDescAbsRapidity (const Particle &a, const Particle &b) |
Sort by descending absolute rapidity,  . . | |
| bool | cmpParticleByAscAbsRapidity (const Particle &a, const Particle &b) |
Sort by ascending absolute rapidity,  . . | |
Stand-alone functions | |
| ParticlePair | beams (const Event &e) |
| Function to get beam particles from an event. | |
| PdgIdPair | beamIds (const Event &e) |
| Function to get beam particle IDs from an event. | |
| PdgIdPair | beamIds (const ParticlePair &beams) |
| Function to get beam particle IDs from a pair of particles. | |
| double | sqrtS (const Event &e) |
| Function to get beam centre of mass energy from an event. | |
| double | sqrtS (const ParticlePair &beams) |
| Function to get beam centre of mass energy from a pair of particles. | |
| double | sqrtS (const FourMomentum &pa, const FourMomentum &pb) |
| Function to get beam centre of mass energy from a pair of beam momenta. | |
Installation directory paths | |
| std::string | getLibPath () |
| Get library install path. | |
| std::string | getDataPath () |
| Get data install path. | |
| std::string | getRivetDataPath () |
| Get Rivet data install path. | |
Analysis library search paths | |
| std::vector< std::string > | getAnalysisLibPaths () |
| Get Rivet analysis plugin library search paths. | |
| void | setAnalysisLibPaths (const std::vector< std::string > &paths) |
| Set the Rivet analysis plugin library search paths. | |
| void | addAnalysisLibPath (const std::string &extrapath) |
| Set the Rivet analysis plugin library search paths. | |
| std::string | findAnalysisLibFile (const std::string &filename) |
| Find the first file of the given name in the analysis library search dirs. | |
Analysis data/metadata paths and search functions | |
| std::vector< std::string > | getAnalysisRefPaths () |
| Get Rivet analysis reference data search paths. | |
| std::string | findAnalysisRefFile (const std::string &filename, const std::vector< std::string > &pathprepend=std::vector< std::string >(), const std::vector< std::string > &pathappend=std::vector< std::string >()) |
| Find the first file of the given name in the ref data file search dirs. | |
| std::vector< std::string > | getAnalysisInfoPaths () |
| Get Rivet analysis info metadata search paths. | |
| std::string | findAnalysisInfoFile (const std::string &filename, const std::vector< std::string > &pathprepend=std::vector< std::string >(), const std::vector< std::string > &pathappend=std::vector< std::string >()) |
| Find the first file of the given name in the analysis info file search dirs. | |
| std::vector< std::string > | getAnalysisPlotPaths () |
| Get Rivet analysis plot style search paths. | |
| std::string | findAnalysisPlotFile (const std::string &filename, const std::vector< std::string > &pathprepend=std::vector< std::string >(), const std::vector< std::string > &pathappend=std::vector< std::string >()) |
| Find the first file of the given name in the analysis plot file search dirs. | |
Variables | |
| static const double | pi = 3.14159265358979323846 |
| static const double | twopi = 2*pi |
| static const double | halfpi = pi/2 |
| static const double | pi2 = pi*pi |
| static const double | Avogadro = 6.0221367e+23/mole |
| static const double | c_light = 2.99792458e+8 * m/s |
| static const double | c_squared = c_light * c_light |
| static const double | h_Planck = 6.6260755e-34 * joule*s |
| static const double | hbar_Planck = h_Planck/twopi |
| static const double | hbarc = hbar_Planck * c_light |
| static const double | hbarc_squared = hbarc * hbarc |
| static const double | electron_charge = - eplus |
| static const double | e_squared = eplus * eplus |
| static const double | electron_mass_c2 = 0.51099906 * MeV |
| static const double | proton_mass_c2 = 938.27231 * MeV |
| static const double | neutron_mass_c2 = 939.56563 * MeV |
| static const double | amu_c2 = 931.49432 * MeV |
| static const double | amu = amu_c2/c_squared |
| static const double | mu0 = 4*pi*1.e-7 * henry/m |
| static const double | epsilon0 = 1./(c_squared*mu0) |
| static const double | elm_coupling = e_squared/(4*pi*epsilon0) |
| static const double | fine_structure_const = elm_coupling/hbarc |
| static const double | classic_electr_radius = elm_coupling/electron_mass_c2 |
| static const double | electron_Compton_length = hbarc/electron_mass_c2 |
| static const double | Bohr_radius = electron_Compton_length/fine_structure_const |
| static const double | alpha_rcl2 |
| static const double | twopi_mc2_rcl2 |
| static const double | k_Boltzmann = 8.617385e-11 * MeV/kelvin |
| static const double | STP_Temperature = 273.15*kelvin |
| static const double | STP_Pressure = 1.*atmosphere |
| static const double | kGasThreshold = 10.*mg/cm3 |
| static const double | universe_mean_density = 1.e-25*g/cm3 |
| const double | MAXDOUBLE = std::numeric_limits<double>::max() |
| const double | MAXINT = std::numeric_limits<int>::max() |
| const double | PI = M_PI |
A pre-defined value of  . . | |
| const double | TWOPI = 2*M_PI |
A pre-defined value of 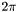 . . | |
| const double | HALFPI = M_PI_2 |
A pre-defined value of 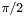 . . | |
| static const double | millimeter = 1. |
| static const double | millimeter2 = millimeter*millimeter |
| static const double | millimeter3 = millimeter*millimeter*millimeter |
| static const double | centimeter = 10.*millimeter |
| static const double | centimeter2 = centimeter*centimeter |
| static const double | centimeter3 = centimeter*centimeter*centimeter |
| static const double | meter = 1000.*millimeter |
| static const double | meter2 = meter*meter |
| static const double | meter3 = meter*meter*meter |
| static const double | kilometer = 1000.*meter |
| static const double | kilometer2 = kilometer*kilometer |
| static const double | kilometer3 = kilometer*kilometer*kilometer |
| static const double | parsec = 3.0856775807e+16*meter |
| static const double | micrometer = 1.e-6 *meter |
| static const double | nanometer = 1.e-9 *meter |
| static const double | angstrom = 1.e-10*meter |
| static const double | picometer = 1.e-12*meter |
| static const double | femtometer = 1.e-15*meter |
| static const double | attometer = 1.e-18*meter |
| static const double | fermi = femtometer |
| static const double | mm = millimeter |
| static const double | mm2 = millimeter2 |
| static const double | mm3 = millimeter3 |
| static const double | cm = centimeter |
| static const double | cm2 = centimeter2 |
| static const double | cm3 = centimeter3 |
| static const double | m = meter |
| static const double | m2 = meter2 |
| static const double | m3 = meter3 |
| static const double | km = kilometer |
| static const double | km2 = kilometer2 |
| static const double | km3 = kilometer3 |
| static const double | pc = parsec |
| static const double | picobarn = 1.0 |
| static const double | barn = 1.0e+12* picobarn |
| static const double | millibarn = 1.0e-3 * barn |
| static const double | microbarn = 1.0e-6 * barn |
| static const double | nanobarn = 1.0e-9 * barn |
| static const double | femtobarn = 1.0e-15 * barn |
| static const double | attobarn = 1.0e-18 * barn |
| static const double | radian = 1. |
| static const double | milliradian = 1.e-3*radian |
| static const double | degree = (3.14159265358979323846/180.0)*radian |
| static const double | steradian = 1. |
| static const double | rad = radian |
| static const double | mrad = milliradian |
| static const double | sr = steradian |
| static const double | deg = degree |
| static const double | nanosecond = 1.0 |
| static const double | second = 1.e+9 *nanosecond |
| static const double | millisecond = 1.e-3 *second |
| static const double | microsecond = 1.e-6 *second |
| static const double | picosecond = 1.e-12*second |
| static const double | hertz = 1.0/second |
| static const double | kilohertz = 1.e+3*hertz |
| static const double | megahertz = 1.e+6*hertz |
| static const double | ns = nanosecond |
| static const double | s = second |
| static const double | ms = millisecond |
| static const double | eplus = 1.0 |
| static const double | e_SI = 1.60217733e-19 |
| static const double | coulomb = eplus/e_SI |
| static const double | gigaelectronvolt = 1. |
| static const double | electronvolt = 1.e-9*gigaelectronvolt |
| static const double | kiloelectronvolt = 1.e-6*gigaelectronvolt |
| static const double | megaelectronvolt = 1.e-3*gigaelectronvolt |
| static const double | teraelectronvolt = 1.e+3*gigaelectronvolt |
| static const double | petaelectronvolt = 1.e+6*gigaelectronvolt |
| static const double | joule = electronvolt/e_SI |
| static const double | eV = electronvolt |
| static const double | keV = kiloelectronvolt |
| static const double | MeV = megaelectronvolt |
| static const double | GeV = gigaelectronvolt |
| static const double | TeV = teraelectronvolt |
| static const double | PeV = petaelectronvolt |
| static const double | eV2 = eV*eV |
| static const double | keV2 = keV*keV |
| static const double | MeV2 = MeV*MeV |
| static const double | GeV2 = GeV*GeV |
| static const double | TeV2 = TeV*TeV |
| static const double | PeV2 = PeV*PeV |
| static const double | kilogram = joule*second*second/(meter*meter) |
| static const double | gram = 1.e-3*kilogram |
| static const double | milligram = 1.e-3*gram |
| static const double | kg = kilogram |
| static const double | g = gram |
| static const double | mg = milligram |
| static const double | watt = joule/second |
| static const double | newton = joule/meter |
| static const double | hep_pascal = newton/m2 |
| static const double | bar = 100000*pascal |
| static const double | atmosphere = 101325*pascal |
| static const double | ampere = coulomb/second |
| static const double | milliampere = 1.e-3*ampere |
| static const double | microampere = 1.e-6*ampere |
| static const double | nanoampere = 1.e-9*ampere |
| static const double | megavolt = megaelectronvolt/eplus |
| static const double | kilovolt = 1.e-3*megavolt |
| static const double | volt = 1.e-6*megavolt |
| static const double | ohm = volt/ampere |
| static const double | farad = coulomb/volt |
| static const double | millifarad = 1.e-3*farad |
| static const double | microfarad = 1.e-6*farad |
| static const double | nanofarad = 1.e-9*farad |
| static const double | picofarad = 1.e-12*farad |
| static const double | weber = volt*second |
| static const double | tesla = volt*second/meter2 |
| static const double | gauss = 1.e-4*tesla |
| static const double | kilogauss = 1.e-1*tesla |
| static const double | henry = weber/ampere |
| static const double | kelvin = 1. |
| static const double | mole = 1. |
| static const double | becquerel = 1./second |
| static const double | curie = 3.7e+10 * becquerel |
| static const double | gray = joule/kilogram |
| static const double | candela = 1. |
| static const double | lumen = candela*steradian |
| static const double | lux = lumen/meter2 |
| static const double | perCent = 0.01 |
| static const double | perThousand = 0.001 |
| static const double | perMillion = 0.000001 |
| static const double | MAXRAPIDITY = 100000.0 |
| A sensible default maximum value of rapidity for Rivet analyses to use. | |
| static const double | MaxRapidity = 100000.0 |
| AnalysisBuilder < ALEPH_1991_S2435284 > | plugin_ALEPH_1991_S2435284 |
| AnalysisBuilder < ALEPH_1996_S3196992 > | plugin_ALEPH_1996_S3196992 |
| AnalysisBuilder < ALEPH_1996_S3486095 > | plugin_ALEPH_1996_S3486095 |
| AnalysisBuilder < ALEPH_2004_S5765862 > | plugin_ALEPH_2004_S5765862 |
| AnalysisBuilder < ALICE_2010_S8624100 > | plugin_ALICE_2010_S8624100 |
| AnalysisBuilder < ALICE_2010_S8625980 > | plugin_ALICE_2010_S8625980 |
| AnalysisBuilder < ALICE_2010_S8706239 > | plugin_ALICE_2010_S8706239 |
| AnalysisBuilder < ATLAS_2010_CONF_2010_049 > | plugin_ATLAS_2010_CONF_2010_049 |
| AnalysisBuilder < ATLAS_2010_S8591806 > | plugin_ATLAS_2010_S8591806 |
| AnalysisBuilder < ATLAS_2010_S8817804 > | plugin_ATLAS_2010_S8817804 |
| AnalysisBuilder < ATLAS_2010_S8894728 > | plugin_ATLAS_2010_S8894728 |
| AnalysisBuilder < ATLAS_2010_S8914702 > | plugin_ATLAS_2010_S8914702 |
| AnalysisBuilder < ATLAS_2010_S8918562 > | plugin_ATLAS_2010_S8918562 |
| AnalysisBuilder < ATLAS_2010_S8919674 > | plugin_ATLAS_2010_S8919674 |
| AnalysisBuilder < ATLAS_2011_CONF_2011_090 > | plugin_ATLAS_2011_CONF_2011_090 |
| AnalysisBuilder < ATLAS_2011_S8924791 > | plugin_ATLAS_2011_S8924791 |
| AnalysisBuilder < ATLAS_2011_S8971293 > | plugin_ATLAS_2011_S8971293 |
| AnalysisBuilder < ATLAS_2011_S8983313 > | plugin_ATLAS_2011_S8983313 |
| AnalysisBuilder < ATLAS_2011_S8994773 > | plugin_ATLAS_2011_S8994773 |
| AnalysisBuilder < ATLAS_2011_S9002537 > | plugin_ATLAS_2011_S9002537 |
| AnalysisBuilder < ATLAS_2011_S9019561 > | plugin_ATLAS_2011_S9019561 |
| AnalysisBuilder < ATLAS_2011_S9120807 > | plugin_ATLAS_2011_S9120807 |
| AnalysisBuilder < BELLE_2006_S6265367 > | plugin_BELLE_2006_S6265367 |
| AnalysisBuilder < CDF_1988_S1865951 > | plugin_CDF_1988_S1865951 |
| AnalysisBuilder < CDF_1990_S2089246 > | plugin_CDF_1990_S2089246 |
| AnalysisBuilder < CDF_1993_S2742446 > | plugin_CDF_1993_S2742446 |
| AnalysisBuilder < CDF_1994_S2952106 > | plugin_CDF_1994_S2952106 |
| AnalysisBuilder < CDF_1996_S3108457 > | plugin_CDF_1996_S3108457 |
| AnalysisBuilder < CDF_1996_S3349578 > | plugin_CDF_1996_S3349578 |
| AnalysisBuilder < CDF_1996_S3418421 > | plugin_CDF_1996_S3418421 |
| AnalysisBuilder < CDF_1997_S3541940 > | plugin_CDF_1997_S3541940 |
| AnalysisBuilder < CDF_1998_S3618439 > | plugin_CDF_1998_S3618439 |
| AnalysisBuilder < CDF_2000_S4155203 > | plugin_CDF_2000_S4155203 |
| AnalysisBuilder < CDF_2000_S4266730 > | plugin_CDF_2000_S4266730 |
| AnalysisBuilder < CDF_2001_S4517016 > | plugin_CDF_2001_S4517016 |
| AnalysisBuilder < CDF_2001_S4563131 > | plugin_CDF_2001_S4563131 |
| AnalysisBuilder < CDF_2001_S4751469 > | plugin_CDF_2001_S4751469 |
| AnalysisBuilder < CDF_2002_S4796047 > | plugin_CDF_2002_S4796047 |
| AnalysisBuilder < CDF_2004_S5839831 > | plugin_CDF_2004_S5839831 |
| AnalysisBuilder < CDF_2005_S6080774 > | plugin_CDF_2005_S6080774 |
| AnalysisBuilder < CDF_2005_S6217184 > | plugin_CDF_2005_S6217184 |
| AnalysisBuilder < CDF_2006_S6450792 > | plugin_CDF_2006_S6450792 |
| AnalysisBuilder < CDF_2006_S6653332 > | plugin_CDF_2006_S6653332 |
| AnalysisBuilder < CDF_2007_S7057202 > | plugin_CDF_2007_S7057202 |
| AnalysisBuilder < CDF_2008_LEADINGJETS > | plugin_CDF_2008_LEADINGJETS |
| AnalysisBuilder < CDF_2008_NOTE_9351 > | plugin_CDF_2008_NOTE_9351 |
| AnalysisBuilder < CDF_2008_S7540469 > | plugin_CDF_2008_S7540469 |
| AnalysisBuilder < CDF_2008_S7541902 > | plugin_CDF_2008_S7541902 |
| AnalysisBuilder < CDF_2008_S7782535 > | plugin_CDF_2008_S7782535 |
| AnalysisBuilder < CDF_2008_S7828950 > | plugin_CDF_2008_S7828950 |
| AnalysisBuilder < CDF_2008_S8093652 > | plugin_CDF_2008_S8093652 |
| AnalysisBuilder < CDF_2008_S8095620 > | plugin_CDF_2008_S8095620 |
| AnalysisBuilder < CDF_2009_NOTE_9936 > | plugin_CDF_2009_NOTE_9936 |
| AnalysisBuilder < CDF_2009_S8057893 > | plugin_CDF_2009_S8057893 |
| AnalysisBuilder < CDF_2009_S8233977 > | plugin_CDF_2009_S8233977 |
| AnalysisBuilder < CDF_2009_S8383952 > | plugin_CDF_2009_S8383952 |
| AnalysisBuilder < CDF_2009_S8436959 > | plugin_CDF_2009_S8436959 |
| AnalysisBuilder < CDF_2010_S8591881_DY > | plugin_CDF_2010_S8591881_DY |
| AnalysisBuilder < CDF_2010_S8591881_QCD > | plugin_CDF_2010_S8591881_QCD |
| AnalysisBuilder < CMS_2010_S8547297 > | plugin_CMS_2010_S8547297 |
| AnalysisBuilder < CMS_2010_S8656010 > | plugin_CMS_2010_S8656010 |
| AnalysisBuilder < CMS_2011_S8884919 > | plugin_CMS_2011_S8884919 |
| AnalysisBuilder < CMS_2011_S8957746 > | plugin_CMS_2011_S8957746 |
| AnalysisBuilder < CMS_2011_S8968497 > | plugin_CMS_2011_S8968497 |
| AnalysisBuilder < CMS_2011_S8978280 > | plugin_CMS_2011_S8978280 |
| AnalysisBuilder< D0_1996_S3214044 > | plugin_D0_1996_S3214044 |
| AnalysisBuilder< D0_1996_S3324664 > | plugin_D0_1996_S3324664 |
| AnalysisBuilder< D0_2000_S4480767 > | plugin_D0_2000_S4480767 |
| AnalysisBuilder< D0_2001_S4674421 > | plugin_D0_2001_S4674421 |
| AnalysisBuilder< D0_2004_S5992206 > | plugin_D0_2004_S5992206 |
| AnalysisBuilder< D0_2006_S6438750 > | plugin_D0_2006_S6438750 |
| AnalysisBuilder< D0_2007_S7075677 > | plugin_D0_2007_S7075677 |
| AnalysisBuilder< D0_2008_S6879055 > | plugin_D0_2008_S6879055 |
| AnalysisBuilder< D0_2008_S7554427 > | plugin_D0_2008_S7554427 |
| AnalysisBuilder< D0_2008_S7662670 > | plugin_D0_2008_S7662670 |
| AnalysisBuilder< D0_2008_S7719523 > | plugin_D0_2008_S7719523 |
| AnalysisBuilder< D0_2008_S7837160 > | plugin_D0_2008_S7837160 |
| AnalysisBuilder< D0_2008_S7863608 > | plugin_D0_2008_S7863608 |
| AnalysisBuilder< D0_2009_S8202443 > | plugin_D0_2009_S8202443 |
| AnalysisBuilder< D0_2009_S8320160 > | plugin_D0_2009_S8320160 |
| AnalysisBuilder< D0_2009_S8349509 > | plugin_D0_2009_S8349509 |
| AnalysisBuilder< D0_2010_S8566488 > | plugin_D0_2010_S8566488 |
| AnalysisBuilder< D0_2010_S8570965 > | plugin_D0_2010_S8570965 |
| AnalysisBuilder< D0_2010_S8671338 > | plugin_D0_2010_S8671338 |
| AnalysisBuilder< D0_2010_S8821313 > | plugin_D0_2010_S8821313 |
| AnalysisBuilder < DELPHI_1995_S3137023 > | plugin_DELPHI_1995_S3137023 |
| AnalysisBuilder < DELPHI_1996_S3430090 > | plugin_DELPHI_1996_S3430090 |
| AnalysisBuilder < DELPHI_2002_069_CONF_603 > | plugin_DELPHI_2002_069_CONF_603 |
| AnalysisBuilder < DELPHI_2003_WUD_03_11 > | plugin_DELPHI_2003_WUD_03_11 |
| AnalysisBuilder < E735_1998_S3905616 > | plugin_E735_1998_S3905616 |
| AnalysisBuilder< ExampleAnalysis > | plugin_ExampleAnalysis |
| AnalysisBuilder< H1_1994_S2919893 > | plugin_H1_1994_S2919893 |
| AnalysisBuilder< H1_1995_S3167097 > | plugin_H1_1995_S3167097 |
| AnalysisBuilder< H1_2000_S4129130 > | plugin_H1_2000_S4129130 |
| AnalysisBuilder < JADE_1998_S3612880 > | plugin_JADE_1998_S3612880 |
| AnalysisBuilder < JADE_OPAL_2000_S4300807 > | plugin_JADE_OPAL_2000_S4300807 |
| AnalysisBuilder < LHCB_2010_S8758301 > | plugin_LHCB_2010_S8758301 |
| AnalysisBuilder< MC_DIJET > | plugin_MC_DIJET |
| AnalysisBuilder< MC_DIPHOTON > | plugin_MC_DIPHOTON |
| AnalysisBuilder< MC_GENERIC > | plugin_MC_GENERIC |
| AnalysisBuilder< MC_HJETS > | plugin_MC_HJETS |
| AnalysisBuilder< MC_JETS > | plugin_MC_JETS |
| AnalysisBuilder< MC_LEADINGJETS > | plugin_MC_LEADINGJETS |
| AnalysisBuilder< MC_PHOTONJETS > | plugin_MC_PHOTONJETS |
| AnalysisBuilder< MC_PHOTONJETUE > | plugin_MC_PHOTONJETUE |
| AnalysisBuilder< MC_SUSY > | plugin_MC_SUSY |
| AnalysisBuilder< MC_TTBAR > | plugin_MC_TTBAR |
| AnalysisBuilder< MC_WJETS > | plugin_MC_WJETS |
| AnalysisBuilder< MC_WPOL > | plugin_MC_WPOL |
| AnalysisBuilder< MC_WWJETS > | plugin_MC_WWJETS |
| AnalysisBuilder< MC_XS > | plugin_MC_XS |
| AnalysisBuilder< MC_ZJETS > | plugin_MC_ZJETS |
| AnalysisBuilder< MC_ZZJETS > | plugin_MC_ZZJETS |
| AnalysisBuilder < OPAL_1993_S2692198 > | plugin_OPAL_1993_S2692198 |
| AnalysisBuilder < OPAL_1998_S3780481 > | plugin_OPAL_1998_S3780481 |
| AnalysisBuilder < OPAL_2001_S4553896 > | plugin_OPAL_2001_S4553896 |
| AnalysisBuilder < OPAL_2004_S6132243 > | plugin_OPAL_2004_S6132243 |
| AnalysisBuilder < PDG_HADRON_MULTIPLICITIES > | plugin_PDG_HADRON_MULTIPLICITIES |
| AnalysisBuilder < PDG_HADRON_MULTIPLICITIES_RATIOS > | plugin_PDG_HADRON_MULTIPLICITIES_RATIOS |
| AnalysisBuilder < SFM_1984_S1178091 > | plugin_SFM_1984_S1178091 |
| AnalysisBuilder < STAR_2006_S6500200 > | plugin_STAR_2006_S6500200 |
| AnalysisBuilder < STAR_2006_S6860818 > | plugin_STAR_2006_S6860818 |
| AnalysisBuilder < STAR_2006_S6870392 > | plugin_STAR_2006_S6870392 |
| AnalysisBuilder < STAR_2008_S7869363 > | plugin_STAR_2008_S7869363 |
| AnalysisBuilder < STAR_2008_S7993412 > | plugin_STAR_2008_S7993412 |
| AnalysisBuilder < STAR_2009_UE_HELEN > | plugin_STAR_2009_UE_HELEN |
| AnalysisBuilder < TASSO_1990_S2148048 > | plugin_TASSO_1990_S2148048 |
| AnalysisBuilder < UA1_1990_S2044935 > | plugin_UA1_1990_S2044935 |
| AnalysisBuilder< UA5_1982_S875503 > | plugin_UA5_1982_S875503 |
| AnalysisBuilder < UA5_1986_S1583476 > | plugin_UA5_1986_S1583476 |
| AnalysisBuilder < UA5_1987_S1640666 > | plugin_UA5_1987_S1640666 |
| AnalysisBuilder < UA5_1988_S1867512 > | plugin_UA5_1988_S1867512 |
| AnalysisBuilder < UA5_1989_S1926373 > | plugin_UA5_1989_S1926373 |
| AnalysisBuilder < ZEUS_2001_S4815815 > | plugin_ZEUS_2001_S4815815 |
Static const convenience particle ID names | |
| static const PdgId | ELECTRON = 11 |
| static const PdgId | POSITRON = -11 |
| static const PdgId | PROTON = 2212 |
| static const PdgId | ANTIPROTON = -2212 |
| static const PdgId | PHOTON = 22 |
| static const PdgId | NEUTRON = 2112 |
| static const PdgId | ANTINEUTRON = -2112 |
| static const PdgId | MUON = 13 |
| static const PdgId | ANTIMUON = -13 |
| static const PdgId | NU_E = 12 |
| static const PdgId | NU_EBAR = -12 |
| static const PdgId | NU_MU = 14 |
| static const PdgId | NU_MUBAR = -14 |
| static const PdgId | NU_TAU = 16 |
| static const PdgId | NU_TAUBAR = -16 |
| static const PdgId | PIPLUS = 211 |
| static const PdgId | PIMINUS = -211 |
| static const PdgId | K0L = 130 |
| static const PdgId | K0S = 310 |
| static const PdgId | KPLUS = 321 |
| static const PdgId | KMINUS = -321 |
| static const PdgId | LAMBDA = 3122 |
| static const PdgId | LAMBDABAR = -3122 |
| static const PdgId | XIMINUS = 3312 |
| static const PdgId | XIPLUS = -3312 |
| static const PdgId | OMEGAMINUS = 3334 |
| static const PdgId | OMEGAPLUS = -3334 |
| static const PdgId | TAU = 15 |
| static const PdgId | ANTITAU = -15 |
| static const PdgId | EMINUS = 11 |
| static const PdgId | EPLUS = -11 |
| static const PdgId | P = 2212 |
| static const PdgId | PBAR = -2212 |
| static const PdgId | GLUON = 21 |
| static const PdgId | GAMMA = 22 |
| static const PdgId | WPLUSBOSON = 24 |
| static const PdgId | WMINUSBOSON = -24 |
| static const PdgId | ZBOSON = 23 |
| static const PdgId | HIGGS = 25 |
| static const PdgId | DQUARK = 1 |
| static const PdgId | UQUARK = 2 |
| static const PdgId | SQUARK = 3 |
| static const PdgId | CQUARK = 4 |
| static const PdgId | BQUARK = 5 |
| static const PdgId | TQUARK = 6 |
| static const PdgId | ANY = 10000 |
Ranges and intervals | |
|
| |
| enum | RangeBoundary { OPEN = 0, SOFT = 0, CLOSED = 1, HARD = 1 } |
| template<typename NUM > | |
| bool | inRange (NUM value, NUM low, NUM high, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=OPEN) |
| Determine if value is in the range low to high, for floating point numbers Interval boundary types are defined by lowbound and highbound. | |
| template<typename NUM > | |
| bool | inRange (NUM value, pair< NUM, NUM > lowhigh, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=OPEN) |
| Alternative version of inRange for doubles, which accepts a pair for the range arguments. | |
| bool | inRange (int value, int low, int high, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=CLOSED) |
| Determine if value is in the range low to high, for integer types Interval boundary types are defined by lowbound and highbound. | |
| bool | inRange (int value, pair< int, int > lowhigh, RangeBoundary lowbound=CLOSED, RangeBoundary highbound=OPEN) |
Alternative version of inRange for ints, which accepts a pair for the range arguments. | |
Detailed Description
- Date:
- 2009-01-30
- Todo:
- Include more projections as required, e.g. ChargedFinalState, FastJets, ZFinder...
- Todo:
- Include more projections as required, e.g. ChargedFinalState, FastJets, ZFinder...
Typedef Documentation
| typedef IsolationProjection<JetAlg, JetAlg> AllJetsIso |
Definition at line 11 of file IsolationTools.hh.
Definition at line 13 of file IsolationTools.hh.
Typedef for Analysis (smart) pointer.
Definition at line 16 of file AnalysisHandler.hh.
| typedef Analysis* AnalysisPtr |
Smart (shared) pointer for handling projections.
Definition at line 10 of file Analysis.fhh.
| typedef std::vector<double> BinEdges |
Typedef for a collection of bin edges.
Definition at line 28 of file RivetAIDA.fhh.
| typedef const Projection* ConstProjectionPtr |
Definition at line 11 of file Projection.fhh.
| typedef std::pair<double, double> doublepair |
Definition at line 11 of file D0_2010_S8570965.cc.
Rivet::Exception is a synonym for Rivet::Error.
Definition at line 19 of file Exceptions.hh.
| typedef std::vector<HistoFormat> HistoFormatList |
Typedef for a collection of histogram format name enums.
Definition at line 44 of file HistoFormat.hh.
| typedef std::map<HistoFormat, std::string> HistoFormatMap |
Typedef for a map of histogram format enums to strings.
Definition at line 14 of file HistoFormat.hh.
| typedef std::map<std::string, HistoFormat> HistoFormatMapR |
Typedef for a map of histogram format name strings to enums.
Definition at line 18 of file HistoFormat.hh.
Definition at line 14 of file MatrixN.hh.
Definition at line 15 of file IsolationTools.hh.
| typedef std::pair<Particle, Particle> ParticlePair |
Typedef for a pair of Particle objects.
Definition at line 20 of file Particle.fhh.
| typedef std::vector<Particle> ParticleVector |
Typedef for a vector of Particle objects.
Definition at line 14 of file Particle.fhh.
| typedef Cmp<Projection> PCmp |
Typedef for Cmp<Projection>
| typedef int PdgId |
Typedef for a PDG ID code.
Definition at line 29 of file Particle.fhh.
Typedef for a pair of particle names.
Definition at line 32 of file Particle.fhh.
| typedef Projection* ProjectionPtr |
Definition at line 9 of file Projection.fhh.
| typedef shared_ptr<const Projection> ProjHandle |
Typedef for Projection (smart) pointer.
Definition at line 14 of file ProjectionHandler.hh.
| typedef vector<fastjet::PseudoJet> PseudoJets |
Typedef for a collection of PseudoJets.
Definition at line 42 of file FastJets.hh.
| typedef boost::minstd_rand RngBase |
Definition at line 31 of file RivetBoost.hh.
| typedef Vector3 ThreeVector |
Definition at line 11 of file Vector3.hh.
| typedef boost::uniform_int UniformIntDist |
Definition at line 34 of file RivetBoost.hh.
| typedef boost::variate_generator<RngBase&, UniformIntDist> UniformIntRNG |
Definition at line 35 of file RivetBoost.hh.
| typedef boost::uniform_real UniformRealDist |
Definition at line 32 of file RivetBoost.hh.
| typedef boost::variate_generator<RngBase&, UniformRealDist> UniformRealRNG |
Definition at line 33 of file RivetBoost.hh.
| typedef FourVector Vector4 |
Definition at line 14 of file Vector4.hh.
Enumeration Type Documentation
| enum CmpState |
Enumerate the possible states of a Cmp object.
Definition at line 14 of file Cmp.fhh.
00014 { 00015 UNDEFINED = -2, //< Undefined state. 00016 ASC = -1, //< The two corresponding objects are in ascending order. 00017 ORDERED = -1, //< The two corresponding objects are ordered. 00018 EQUIVALENT = 0, //< The two corresponding objects are equivalent. 00019 DESC = 1, //< The two corresponding objects are in descending order. 00020 UNORDERED = 1, //< The two corresponding objects are anti-ordered. 00021 ANTIORDERED = 1 //< The two corresponding objects are anti-ordered. 00022 };
| enum HistoFormat |
Enumeration of available histogram output formats.
Definition at line 11 of file HistoFormat.hh.
| enum PhiMapping |
Enum for range of  to be mapped into.
to be mapped into.
Definition at line 60 of file MathHeader.hh.
00060 { MINUSPI_PLUSPI, ZERO_2PI };
| enum RangeBoundary |
Represents whether an interval is open (non-inclusive) or closed (inclusive). For example, the interval 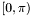 is closed (an inclusive boundary) at 0, and open (a non-inclusive boundary) at
is closed (an inclusive boundary) at 0, and open (a non-inclusive boundary) at  .
.
Definition at line 92 of file MathUtils.hh.
| enum RapScheme |
Enum for rapidity variable to be used in calculating 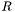 , applying rapidity cuts, etc.
, applying rapidity cuts, etc.
Definition at line 57 of file MathHeader.hh.
00057 { PSEUDORAPIDITY = 0, ETA = 0, RAPIDITY = 1, YRAP = 1 };
| enum Sign |
Enum for signs of numbers.
Definition at line 54 of file MathHeader.hh.
Function Documentation
| void Rivet::_calcS | ( | const vector< Vector3 > & | perpmomenta, | |
| double & | sphero, | |||
| Vector3 & | saxis | |||
| ) |
Definition at line 64 of file Spherocity.cc.
References cross(), Vector< N >::mod(), s, Vector< N >::size(), Vector3::x(), and Vector3::y().
Referenced by Spherocity::_calcSpherocity().
00064 { 00065 // According to the Salam paper, p5, footnote 4, the 00066 // axis n that minimises the Spherocity value ALWAYS coincides with the 00067 // direction of one of the transverse momentum vectors of the events particles. 00068 // Thus we carry out the calculation of Sphero for all particles and pick the 00069 // one that yields the smallerst values 00070 00071 vector<Vector3> p = perpmomenta; 00072 vector<double> sval; 00073 00074 00075 // Prepare vector to store unit vector representation of all particle momenta 00076 // and also calculate the transverse momentum sum 00077 vector<Vector3> units; 00078 double sumperpmomenta = 0.0; 00079 foreach (const Vector3& p, perpmomenta) { 00080 units.push_back(Vector3(p.x(), p.y(), 0.0).unit()); 00081 sumperpmomenta += p.mod(); 00082 } 00083 00084 // Spherocity calculation 00085 // 00086 // The outer loop is for iteration over all unit vectors 00087 foreach (const Vector3& u, units){ 00088 double s =0.0; 00089 for (unsigned int k=0 ; k<p.size() ; k++) 00090 s += fabs(p[k].cross(u).mod() ); 00091 00092 sval.push_back(s); 00093 } 00094 00095 00096 // Pick the solution with the smallest spherocity 00097 sphero = 999.; 00098 for (unsigned int i=0 ; i<units.size() ; i++) 00099 if (sval[i] < sphero){ 00100 sphero = sval[i]; 00101 saxis = units[i]; 00102 } 00103 00104 }
| void Rivet::_calcT | ( | const vector< Vector3 > & | momenta, | |
| double & | t, | |||
| Vector3 & | taxis | |||
| ) |
Definition at line 48 of file Thrust.cc.
References Vector3::dot(), mod(), mod2Cmp(), Rivet::PID::n, sign(), and Vector3::unit().
Referenced by Thrust::_calcThrust().
00048 { 00049 /* This function implements the iterative algorithm as described in the 00050 * Pythia manual. We take eight (four) different starting vectors 00051 * constructed from the four (three) leading particles to make sure that 00052 * we don't find a local maximum. 00053 */ 00054 vector<Vector3> p = momenta; 00055 assert(p.size() >= 3); 00056 unsigned int n = 3; 00057 if (p.size() == 3) n = 3; 00058 vector<Vector3> tvec; 00059 vector<double> tval; 00060 std::sort(p.begin(), p.end(), mod2Cmp); 00061 for (unsigned int i=0 ; i<pow(2,n-1) ; i++) { 00062 // Create an initial vector from the leading four jets 00063 Vector3 foo(0,0,0); 00064 int sign=i; 00065 for (unsigned int k=0 ; k<n ; k++) { 00066 (sign%2)==1 ? foo+=p[k] : foo-=p[k]; 00067 sign/=2; 00068 } 00069 foo=foo.unit(); 00070 00071 // Iterate 00072 double diff=999.; 00073 while (diff>1e-5) { 00074 Vector3 foobar(0,0,0); 00075 for (unsigned int k=0 ; k<p.size() ; k++) 00076 foo.dot(p[k])>0 ? foobar+=p[k] : foobar-=p[k]; 00077 diff=(foo-foobar.unit()).mod(); 00078 foo=foobar.unit(); 00079 } 00080 00081 // Calculate the thrust value for the vector we found 00082 t=0.; 00083 for (unsigned int k=0 ; k<p.size() ; k++) 00084 t+=fabs(foo.dot(p[k])); 00085 00086 // Store everything 00087 tval.push_back(t); 00088 tvec.push_back(foo); 00089 } 00090 00091 // Pick the solution with the largest thrust 00092 t=0.; 00093 for (unsigned int i=0 ; i<tvec.size() ; i++) 00094 if (tval[i]>t){ 00095 t=tval[i]; 00096 taxis=tvec[i]; 00097 } 00098 }
| string Rivet::_findFile | ( | const string & | filename, | |
| const vector< string > & | paths | |||
| ) | [inline] |
Definition at line 9 of file RivetPaths.cc.
| void Rivet::_geRot180x | ( | GenEvent & | ge | ) |
Definition at line 10 of file Event.cc.
Referenced by Event::_geNormAlignment().
00010 { 00011 for (HepMC::GenEvent::particle_iterator ip = ge.particles_begin(); ip != ge.particles_end(); ++ip) { 00012 const HepMC::FourVector& mom = (*ip)->momentum(); 00013 (*ip)->set_momentum(HepMC::FourVector(mom.px(), -mom.py(), -mom.pz(), mom.e())); 00014 } 00015 for (HepMC::GenEvent::vertex_iterator iv = ge.vertices_begin(); iv != ge.vertices_end(); ++iv) { 00016 const HepMC::FourVector& pos = (*iv)->position(); 00017 (*iv)->set_position(HepMC::FourVector(pos.x(), -pos.y(), -pos.z(), pos.t())); 00018 } 00019 }
| double Rivet::_mapAngleM2PITo2Pi | ( | double | angle | ) | [inline] |
Reduce any number to the range [-2PI, 2PI] by repeated addition or subtraction of 2PI as required. Used to normalise angular measures.
Definition at line 345 of file MathUtils.hh.
References isZero(), and TWOPI.
Referenced by mapAngle0To2Pi(), and mapAngleMPiToPi().
| void Rivet::_updateLevels | ( | const Log::LevelMap & | defaultLevels, | |
| Log::LogMap & | existingLogs | |||
| ) |
- Todo:
- Add single static setLevel
- Todo:
- Check ordering - "Foo" should come before "Foo.Bar"
Definition at line 28 of file Logging.cc.
Referenced by Log::setLevel(), and Log::setLevels().
00028 { 00029 /// @todo Check ordering - "Foo" should come before "Foo.Bar" 00030 for (Log::LevelMap::const_iterator lev = defaultLevels.begin(); lev != defaultLevels.end(); ++lev) { 00031 for (Log::LogMap::iterator log = existingLogs.begin(); log != existingLogs.end(); ++log) { 00032 if (log->first.find(lev->first) == 0) { 00033 log->second->setLevel(lev->second); 00034 } 00035 } 00036 } 00037 }
| FourMomentum Rivet::add | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 523 of file Vector4.hh.
References Vector< N >::_vec.
| FourVector Rivet::add | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Definition at line 225 of file Vector4.hh.
References Vector< N >::_vec.
| Vector3 add | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Definition at line 246 of file Vector3.hh.
References Vector< N >::_vec.
| Matrix<N> Rivet::add | ( | const Matrix< N > & | a, | |
| const Matrix< N > & | b | |||
| ) | [inline] |
Definition at line 262 of file MatrixN.hh.
References Matrix< N >::_matrix.
Referenced by operator+(), operator-(), and subtract().
| Num Rivet::add_quad | ( | Num | a, | |
| Num | b, | |||
| Num | c | |||
| ) | [inline] |
Named number-type addition in quadrature operation.
Definition at line 162 of file MathUtils.hh.
| Num Rivet::add_quad | ( | Num | a, | |
| Num | b | |||
| ) | [inline] |
Named number-type addition in quadrature operation.
Definition at line 156 of file MathUtils.hh.
| void addAnalysisLibPath | ( | const std::string & | extrapath | ) |
Set the Rivet analysis plugin library search paths.
Definition at line 51 of file RivetPaths.cc.
00053 { 00054 vector<string> paths = getAnalysisLibPaths(); 00055 paths.push_back(extrapath);
| double Rivet::angle | ( | const FourVector & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Angle (in radians) between spatial parts of two Lorentz vectors.
Definition at line 256 of file Vector4.hh.
References FourVector::angle().
| double Rivet::angle | ( | const Vector3 & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Angle (in radians) between spatial parts of two Lorentz vectors.
Definition at line 251 of file Vector4.hh.
References angle(), and FourVector::vector3().
00251 { 00252 return angle( a, b.vector3() ); 00253 }
| double Rivet::angle | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Angle (in radians) between spatial parts of two Lorentz vectors.
Definition at line 246 of file Vector4.hh.
References FourVector::angle().
| double Rivet::angle | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Angle (in radians) between two 3-vectors.
Definition at line 269 of file Vector3.hh.
References Vector3::angle().
Referenced by MC_DIJET::analyze(), angle(), DISKinematics::project(), and Matrix3::setAsRotation().
| double Rivet::azimuthalAngle | ( | const FourVector & | v, | |
| const PhiMapping | mapping = ZERO_2PI | |||
| ) | [inline] |
Calculate azimuthal angle of a Lorentz vector.
Definition at line 287 of file Vector4.hh.
References FourVector::azimuthalAngle().
| double Rivet::azimuthalAngle | ( | const Vector3 & | v, | |
| const PhiMapping | mapping = ZERO_2PI | |||
| ) | [inline] |
Calculate azimuthal angle of a 3-vector. Returns a number in (-pi, pi] or in [0, 2pi) according to the mapping scheme selected.
Definition at line 302 of file Vector3.hh.
References Vector3::azimuthalAngle().
Referenced by MC_DIJET::analyze(), CDF_2010_S8591881_DY::analyze(), and CDF_2008_NOTE_9351::analyze().
| PdgIdPair beamIds | ( | const ParticlePair & | beams | ) |
| PdgIdPair beamIds | ( | const Event & | e | ) |
Function to get beam particle IDs from an event.
Definition at line 15 of file Beam.cc.
References Beam::beamIds(), and Beam::project().
| ParticlePair beams | ( | const Event & | e | ) |
Function to get beam particles from an event.
Definition at line 9 of file Beam.cc.
References Beam::beams(), and Beam::project().
Referenced by AnalysisHandler::init(), DISLepton::project(), and DISKinematics::project().
| Vector3 Rivet::boostVector | ( | const FourMomentum & | v | ) | [inline] |
Calculate the velocity boost vector of a momentum 4-vector.
Definition at line 584 of file Vector4.hh.
References FourMomentum::boostVector().
| bool Rivet::chargedParticleFilter | ( | const Particle & | p | ) |
Definition at line 35 of file ChargedFinalState.cc.
References Particle::pdgId(), and Rivet::PID::threeCharge().
Referenced by ChargedFinalState::project().
00035 { 00036 return PID::threeCharge(p.pdgId()) == 0; 00037 }
| Cmp<T> Rivet::cmp | ( | const T & | t1, | |
| const T & | t2 | |||
| ) | [inline] |
Global helper function for easy creation of Cmp objects.
Definition at line 282 of file Cmp.hh.
Referenced by ZFinder::compare(), WFinder::compare(), VetoedFinalState::compare(), UnstableFinalState::compare(), SVertex::compare(), Sphericity::compare(), NeutralFinalState::compare(), LeptonClusters::compare(), JetShape::compare(), IsolationProjection< PROJ1, PROJ2, EST >::compare(), InvMassFinalState::compare(), IdentifiedFinalState::compare(), FinalState::compare(), FastJets::compare(), ConstRandomFilter::compare(), and ClusteredPhotons::compare().
| bool Rivet::cmpJetsByAscAbsPseudorapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 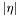 (ascending) Use this so that lowest
(ascending) Use this so that lowest 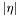 is at the front of the list.
is at the front of the list.
Definition at line 239 of file Jet.hh.
References Jet::momentum(), and FourVector::pseudorapidity().
| bool Rivet::cmpJetsByAscAbsRapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by  (ascending) Use this so that lowest
(ascending) Use this so that lowest  is at the front of the list.
is at the front of the list.
Definition at line 261 of file Jet.hh.
References Jet::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpJetsByAscE | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 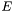 (ascending) Use this so that lowest
(ascending) Use this so that lowest 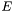 is at the front of the list.
is at the front of the list.
Definition at line 217 of file Jet.hh.
References FourMomentum::E(), and Jet::momentum().
| bool Rivet::cmpJetsByAscP | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by ascending momentum, 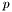 .
.
Definition at line 195 of file Jet.hh.
References Vector< N >::mod(), Jet::momentum(), and FourVector::vector3().
| bool Rivet::cmpJetsByAscPseudorapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 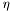 (ascending) Use this so that lowest
(ascending) Use this so that lowest 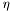 is at the front of the list.
is at the front of the list.
Definition at line 228 of file Jet.hh.
References Jet::momentum(), and FourVector::pseudorapidity().
| bool Rivet::cmpJetsByAscPt | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 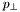 (ascending) Use this so that lowest
(ascending) Use this so that lowest 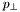 is at the front of the list.
is at the front of the list.
Definition at line 186 of file Jet.hh.
References Jet::ptSum().
| bool Rivet::cmpJetsByAscRapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 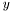 (ascending) Use this so that lowest
(ascending) Use this so that lowest 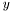 is at the front of the list.
is at the front of the list.
Definition at line 250 of file Jet.hh.
References Jet::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpJetsByDescAbsPseudorapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 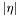 (descending) Use this so that highest
(descending) Use this so that highest 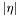 is at the front of the list.
is at the front of the list.
Definition at line 234 of file Jet.hh.
References Jet::momentum(), and FourVector::pseudorapidity().
| bool Rivet::cmpJetsByDescAbsRapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by  (descending) Use this so that highest
(descending) Use this so that highest  is at the front of the list.
is at the front of the list.
Definition at line 256 of file Jet.hh.
References Jet::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpJetsByDescPseudorapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 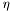 (descending) Use this so that highest
(descending) Use this so that highest 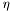 is at the front of the list.
is at the front of the list.
Definition at line 223 of file Jet.hh.
References Jet::momentum(), and FourVector::pseudorapidity().
| bool Rivet::cmpJetsByDescRapidity | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 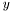 (descending) Use this so that highest
(descending) Use this so that highest 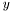 is at the front of the list.
is at the front of the list.
Definition at line 245 of file Jet.hh.
References Jet::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpJetsByE | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 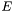 (descending - usual sorting for HEP) Use this so that highest
(descending - usual sorting for HEP) Use this so that highest 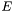 is at the front of the list.
is at the front of the list.
Definition at line 212 of file Jet.hh.
References FourMomentum::E(), and Jet::momentum().
Referenced by JetAlg::jetsByE().
| bool Rivet::cmpJetsByEt | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Use this so that highest 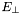 is at the front of the list.
is at the front of the list.
Definition at line 201 of file Jet.hh.
References Jet::EtSum().
Referenced by JetAlg::jetsByEt().
| bool Rivet::cmpJetsByEtDesc | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Use this so that lowest 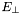 is at the front of the list.
is at the front of the list.
Definition at line 206 of file Jet.hh.
References Jet::EtSum().
| bool Rivet::cmpJetsByP | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by descending momentum, 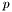 .
.
Definition at line 191 of file Jet.hh.
References Vector< N >::mod(), Jet::momentum(), and FourVector::vector3().
Referenced by JetAlg::jetsByP().
| bool Rivet::cmpJetsByPt | ( | const Jet & | a, | |
| const Jet & | b | |||
| ) | [inline] |
Compare jets by 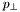 (descending - usual sorting for HEP) Use this so that highest
(descending - usual sorting for HEP) Use this so that highest 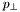 is at the front of the list.
is at the front of the list.
Definition at line 181 of file Jet.hh.
References Jet::ptSum().
Referenced by CDF_2008_S7540469::analyze(), and JetAlg::jetsByPt().
| bool Rivet::cmpMomByAscAbsPseudorapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 47 of file JetAlg.hh.
References FourVector::pseudorapidity().
| bool Rivet::cmpMomByAscAbsRapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 59 of file JetAlg.hh.
References FourMomentum::rapidity().
| bool Rivet::cmpMomByAscE | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 35 of file JetAlg.hh.
References FourMomentum::E().
| bool Rivet::cmpMomByAscEt | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 29 of file JetAlg.hh.
References FourMomentum::Et().
| bool Rivet::cmpMomByAscP | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 23 of file JetAlg.hh.
References Vector< N >::mod(), and FourVector::vector3().
| bool Rivet::cmpMomByAscPseudorapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 41 of file JetAlg.hh.
References FourVector::pseudorapidity().
| bool Rivet::cmpMomByAscPt | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 17 of file JetAlg.hh.
References FourMomentum::pT().
| bool Rivet::cmpMomByAscRapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 53 of file JetAlg.hh.
References FourMomentum::rapidity().
| bool Rivet::cmpMomByDescAbsPseudorapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 44 of file JetAlg.hh.
References FourVector::pseudorapidity().
| bool Rivet::cmpMomByDescAbsRapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 56 of file JetAlg.hh.
References FourMomentum::rapidity().
| bool Rivet::cmpMomByDescPseudorapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 38 of file JetAlg.hh.
References FourVector::pseudorapidity().
| bool Rivet::cmpMomByDescRapidity | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 50 of file JetAlg.hh.
References FourMomentum::rapidity().
| bool Rivet::cmpMomByE | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 32 of file JetAlg.hh.
References FourMomentum::E().
| bool Rivet::cmpMomByEt | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 26 of file JetAlg.hh.
References FourMomentum::Et().
| bool Rivet::cmpMomByP | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 20 of file JetAlg.hh.
References Vector< N >::mod(), and FourVector::vector3().
| bool Rivet::cmpMomByPt | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 14 of file JetAlg.hh.
References FourMomentum::pT().
| bool Rivet::cmpParticleByAscAbsPseudorapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending absolute pseudorapidity, 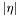 .
.
Definition at line 180 of file Particle.hh.
References Particle::momentum(), and FourVector::pseudorapidity().
Referenced by FinalState::particlesByModEta().
| bool Rivet::cmpParticleByAscAbsRapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending absolute rapidity,  .
.
Definition at line 196 of file Particle.hh.
References Particle::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpParticleByAscE | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending energy, 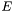 .
.
Definition at line 164 of file Particle.hh.
References FourMomentum::E(), and Particle::momentum().
| bool Rivet::cmpParticleByAscEt | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending transverse energy, 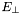 .
.
Definition at line 156 of file Particle.hh.
References FourMomentum::Et(), and Particle::momentum().
| bool Rivet::cmpParticleByAscP | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending momentum, 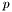 .
.
Definition at line 148 of file Particle.hh.
References Vector< N >::mod(), Particle::momentum(), and FourVector::vector3().
| bool Rivet::cmpParticleByAscPseudorapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending pseudorapidity, 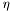 .
.
Definition at line 172 of file Particle.hh.
References Particle::momentum(), and FourVector::pseudorapidity().
Referenced by FinalState::particlesByEta().
| bool Rivet::cmpParticleByAscPt | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending transverse momentum, 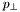 .
.
Definition at line 140 of file Particle.hh.
References Particle::momentum(), and FourMomentum::pT().
| bool Rivet::cmpParticleByAscRapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by ascending rapidity, 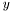 .
.
Definition at line 188 of file Particle.hh.
References Particle::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpParticleByDescAbsPseudorapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending absolute pseudorapidity, 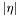 .
.
Definition at line 176 of file Particle.hh.
References Particle::momentum(), and FourVector::pseudorapidity().
| bool Rivet::cmpParticleByDescAbsRapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending absolute rapidity,  .
.
Definition at line 192 of file Particle.hh.
References Particle::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpParticleByDescPseudorapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending pseudorapidity, 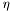 .
.
Definition at line 168 of file Particle.hh.
References Particle::momentum(), and FourVector::pseudorapidity().
| bool Rivet::cmpParticleByDescRapidity | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending rapidity, 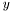 .
.
Definition at line 184 of file Particle.hh.
References Particle::momentum(), and FourMomentum::rapidity().
| bool Rivet::cmpParticleByE | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending energy, 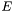 .
.
Definition at line 160 of file Particle.hh.
References FourMomentum::E(), and Particle::momentum().
Referenced by FinalState::particlesByE().
| bool Rivet::cmpParticleByEt | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending transverse energy, 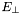 .
.
Definition at line 152 of file Particle.hh.
References FourMomentum::Et(), and Particle::momentum().
Referenced by FinalState::particlesByEt().
| bool Rivet::cmpParticleByP | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending momentum, 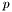 .
.
Definition at line 144 of file Particle.hh.
References Vector< N >::mod(), Particle::momentum(), and FourVector::vector3().
Referenced by FinalState::particlesByP().
| bool Rivet::cmpParticleByPt | ( | const Particle & | a, | |
| const Particle & | b | |||
| ) | [inline] |
Sort by descending transverse momentum, 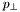 .
.
Definition at line 136 of file Particle.hh.
References Particle::momentum(), and FourMomentum::pT().
Referenced by D0_2010_S8821313::analyze(), D0_2010_S8570965::analyze(), ATLAS_2011_S9120807::analyze(), ATLAS_2011_CONF_2011_090::analyze(), and FinalState::particlesByPt().
| LorentzTransform Rivet::combine | ( | const LorentzTransform & | a, | |
| const LorentzTransform & | b | |||
| ) | [inline] |
Definition at line 153 of file LorentzTrans.hh.
References LorentzTransform::combine().
| bool Rivet::compatible | ( | const PdgIdPair & | pair, | |
| const set< PdgIdPair > & | allowedpairs | |||
| ) | [inline] |
Find whether a PdgIdPair pair is compatible with at least one template beam pair in a set allowedpairs.
Definition at line 48 of file BeamConstraint.hh.
References compatible().
00048 { 00049 for (set<PdgIdPair>::const_iterator bp = allowedpairs.begin(); bp != allowedpairs.end(); ++bp) { 00050 if (compatible(pair, *bp)) return true; 00051 } 00052 return false; 00053 }
| bool Rivet::compatible | ( | const PdgIdPair & | allowedpair, | |
| const ParticlePair & | ppair | |||
| ) | [inline] |
Check particle compatibility of Particle pairs (for symmetric completeness).
Definition at line 40 of file BeamConstraint.hh.
References compatible().
00041 { 00042 return compatible(ppair, allowedpair); 00043 }
| bool Rivet::compatible | ( | const ParticlePair & | ppair, | |
| const PdgIdPair & | allowedpair | |||
| ) | [inline] |
Check particle compatibility of Particle pairs.
Definition at line 34 of file BeamConstraint.hh.
References compatible(), and make_pdgid_pair().
00035 { 00036 return compatible(make_pdgid_pair(ppair.first.pdgId(), 00037 ppair.second.pdgId()), allowedpair); 00038 }
| bool Rivet::compatible | ( | const PdgIdPair & | pair, | |
| const PdgIdPair & | allowedpair | |||
| ) | [inline] |
Find whether PdgIdPair pair is compatible with the template PdgIdPair allowedpair. This assesses whether either of the two possible pairings of pair's constituents is compatible.
Definition at line 24 of file BeamConstraint.hh.
References compatible().
00024 { 00025 bool oneToOne = compatible(pair.first, allowedpair.first); 00026 bool twoToTwo = compatible(pair.second, allowedpair.second); 00027 bool oneToTwo = compatible(pair.first, allowedpair.second); 00028 bool twoToOne = compatible(pair.second, allowedpair.first); 00029 return (oneToOne && twoToTwo) || (oneToTwo && twoToOne); 00030 }
| bool Rivet::compatible | ( | PdgId | p, | |
| PdgId | allowed | |||
| ) | [inline] |
Find whether ParticleName p is compatible with the template ParticleName allowed. Effectively this is asking whether p is a subset of allowed.
Definition at line 16 of file BeamConstraint.hh.
References ANY.
Referenced by AnalysisHandler::analyze(), compatible(), and intersection().
00016 { 00017 //assert(p != ANY); 00018 return (allowed == ANY || p == allowed); 00019 }
| double Rivet::contract | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Contract two 4-vectors, with metric signature (+ - - -).
Definition at line 194 of file Vector4.hh.
References FourVector::contract().
Referenced by dot().
| double Rivet::correlation | ( | const vector< int > & | sample1, | |
| const vector< int > & | sample2 | |||
| ) | [inline] |
Calculate the correlation strength between two samples.
Definition at line 306 of file MathUtils.hh.
References covariance().
Referenced by correlation_err(), and UA5_1988_S1867512::finalize().
00306 { 00307 const double cov = covariance(sample1, sample2); 00308 const double var1 = covariance(sample1, sample1); 00309 const double var2 = covariance(sample2, sample2); 00310 const double correlation = cov/sqrt(var1*var2); 00311 const double corr_strength = correlation*sqrt(var2/var1); 00312 return corr_strength; 00313 }
| double Rivet::correlation_err | ( | const vector< int > & | sample1, | |
| const vector< int > & | sample2 | |||
| ) | [inline] |
Calculate the error of the correlation strength between two samples assuming Poissonian errors.
Definition at line 316 of file MathUtils.hh.
References correlation(), covariance(), and covariance_err().
Referenced by UA5_1988_S1867512::finalize().
00316 { 00317 const double cov = covariance(sample1, sample2); 00318 const double var1 = covariance(sample1, sample1); 00319 const double var2 = covariance(sample2, sample2); 00320 const double cov_e = covariance_err(sample1, sample2); 00321 const double var1_e = covariance_err(sample1, sample1); 00322 const double var2_e = covariance_err(sample2, sample2); 00323 00324 // Calculate the correlation 00325 const double correlation = cov/sqrt(var1*var2); 00326 // Calculate the error on the correlation 00327 const double correlation_err = cov_e/sqrt(var1*var2) - 00328 cov/(2*pow(3./2., var1*var2)) * (var1_e * var2 + var1 * var2_e); 00329 00330 00331 // Calculate the error on the correlation strength 00332 const double corr_strength_err = correlation_err*sqrt(var2/var1) + 00333 correlation/(2*sqrt(var2/var1)) * (var2_e/var1 - var2*var1_e/pow(2, var2)); 00334 00335 return corr_strength_err; 00336 }
| double Rivet::covariance | ( | const vector< int > & | sample1, | |
| const vector< int > & | sample2 | |||
| ) | [inline] |
Calculate the covariance (variance) between two samples.
Definition at line 274 of file MathUtils.hh.
References mean().
Referenced by correlation(), and correlation_err().
00274 { 00275 const double mean1 = mean(sample1); 00276 const double mean2 = mean(sample2); 00277 const int N = sample1.size(); 00278 double cov = 0.0; 00279 for (int i = 0; i < N; i++) { 00280 const double cov_i = (sample1[i] - mean1)*(sample2[i] - mean2); 00281 cov += cov_i; 00282 } 00283 if (N > 1) return cov/(N-1); 00284 else return 0.0; 00285 }
| double Rivet::covariance_err | ( | const vector< int > & | sample1, | |
| const vector< int > & | sample2 | |||
| ) | [inline] |
Calculate the error on the covariance (variance) of two samples, assuming poissonian errors.
Definition at line 288 of file MathUtils.hh.
References mean(), and mean_err().
Referenced by correlation_err().
00288 { 00289 const double mean1 = mean(sample1); 00290 const double mean2 = mean(sample2); 00291 const double mean1_e = mean_err(sample1); 00292 const double mean2_e = mean_err(sample2); 00293 const int N = sample1.size(); 00294 double cov_e = 0.0; 00295 for (int i = 0; i < N; i++) { 00296 const double cov_i = (sqrt(sample1[i]) - mean1_e)*(sample2[i] - mean2) + 00297 (sample1[i] - mean1)*(sqrt(sample2[i]) - mean2_e); 00298 cov_e += cov_i; 00299 } 00300 if (N > 1) return cov_e/(N-1); 00301 else return 0.0; 00302 }
| AIDA::IAnalysisFactory * createAnalysisFactory | ( | ) |
Get an AIDA system (LWH impl.).
Definition at line 16 of file RivetAIDA.cc.
Referenced by AnalysisHandler::AnalysisHandler().
| Vector3 Rivet::cross | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Definition at line 220 of file Vector3.hh.
References Vector3::cross().
Referenced by _calcS(), Spherocity::_calcSpherocity(), Thrust::_calcThrust(), and Matrix3::setAsRotation().
| double Rivet::deltaEta | ( | double | eta, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 312 of file Particle.hh.
References deltaEta(), and Particle::momentum().
| double Rivet::deltaEta | ( | const Vector3 & | v, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 308 of file Particle.hh.
References deltaEta(), and Particle::momentum().
00308 { 00309 return deltaEta(v, p.momentum()); 00310 }
| double Rivet::deltaEta | ( | const FourVector & | v, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 304 of file Particle.hh.
References deltaEta(), and Particle::momentum().
00304 { 00305 return deltaEta(v, p.momentum()); 00306 }
| double Rivet::deltaEta | ( | const FourMomentum & | v, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 300 of file Particle.hh.
References deltaEta(), and Particle::momentum().
00300 { 00301 return deltaEta(v, p.momentum()); 00302 }
| double Rivet::deltaEta | ( | const Particle & | p, | |
| double | eta | |||
| ) | [inline] |
Definition at line 296 of file Particle.hh.
References deltaEta(), and Particle::momentum().
| double Rivet::deltaEta | ( | const Particle & | p, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 292 of file Particle.hh.
References deltaEta(), and Particle::momentum().
00292 { 00293 return deltaEta(p.momentum(), v); 00294 }
| double Rivet::deltaEta | ( | const Particle & | p, | |
| const FourVector & | v | |||
| ) | [inline] |
Definition at line 288 of file Particle.hh.
References deltaEta(), and Particle::momentum().
00288 { 00289 return deltaEta(p.momentum(), v); 00290 }
| double Rivet::deltaEta | ( | const Particle & | p, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Definition at line 284 of file Particle.hh.
References deltaEta(), and Particle::momentum().
00284 { 00285 return deltaEta(p.momentum(), v); 00286 }
| double Rivet::deltaEta | ( | const Particle & | p1, | |
| const Particle & | p2 | |||
| ) | [inline] |
Definition at line 280 of file Particle.hh.
References deltaEta(), and Particle::momentum().
00280 { 00281 return deltaEta(p1.momentum(), p2.momentum()); 00282 }
| double Rivet::deltaEta | ( | const Vector3 & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 913 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00913 { 00914 return deltaEta(a, b.vector3()); 00915 }
| double Rivet::deltaEta | ( | const FourMomentum & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 908 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00908 { 00909 return deltaEta(a.vector3(), b); 00910 }
| double Rivet::deltaEta | ( | const Vector3 & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 903 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00903 { 00904 return deltaEta(a, b.vector3()); 00905 }
| double Rivet::deltaEta | ( | const FourVector & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 898 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00898 { 00899 return deltaEta(a.vector3(), b); 00900 }
| double Rivet::deltaEta | ( | const FourMomentum & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 893 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00893 { 00894 return deltaEta(a.vector3(), b.vector3()); 00895 }
| double Rivet::deltaEta | ( | const FourVector & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 888 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00888 { 00889 return deltaEta(a.vector3(), b.vector3()); 00890 }
| double Rivet::deltaEta | ( | double | eta1, | |
| const FourVector & | v | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 883 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00883 { 00884 return deltaEta(eta1, v.vector3()); 00885 }
| double Rivet::deltaEta | ( | const FourVector & | v, | |
| double | eta2 | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 878 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00878 { 00879 return deltaEta(v.vector3(), eta2); 00880 }
| double Rivet::deltaEta | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 873 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00873 { 00874 return deltaEta(a.vector3(), b.vector3()); 00875 }
| double Rivet::deltaEta | ( | double | eta1, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 868 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00868 { 00869 return deltaEta(eta1, v.vector3()); 00870 }
| double Rivet::deltaEta | ( | const FourMomentum & | v, | |
| double | eta2 | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 863 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00863 { 00864 return deltaEta(v.vector3(), eta2); 00865 }
| double Rivet::deltaEta | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 858 of file Vector4.hh.
References deltaEta(), and FourVector::vector3().
00858 { 00859 return deltaEta(a.vector3(), b.vector3()); 00860 }
| double Rivet::deltaEta | ( | double | eta1, | |
| const Vector3 & | v | |||
| ) | [inline] |
Calculate the difference in pseudorapidity between two spatial vectors.
Definition at line 345 of file Vector3.hh.
References deltaEta(), and Vector3::pseudorapidity().
00345 { 00346 return deltaEta(eta1, v.pseudorapidity()); 00347 }
| double Rivet::deltaEta | ( | const Vector3 & | v, | |
| double | eta2 | |||
| ) | [inline] |
Calculate the difference in pseudorapidity between two spatial vectors.
Definition at line 340 of file Vector3.hh.
References deltaEta(), and Vector3::pseudorapidity().
00340 { 00341 return deltaEta(v.pseudorapidity(), eta2); 00342 }
| double Rivet::deltaEta | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the difference in pseudorapidity between two spatial vectors.
Definition at line 335 of file Vector3.hh.
References deltaEta(), and Vector3::pseudorapidity().
00335 { 00336 return deltaEta(a.pseudorapidity(), b.pseudorapidity()); 00337 }
| double Rivet::deltaEta | ( | double | eta1, | |
| double | eta2 | |||
| ) | [inline] |
Calculate the difference between two pseudorapidities, returning the unsigned value.
Definition at line 394 of file MathUtils.hh.
| double Rivet::deltaEta | ( | double | eta, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 404 of file Jet.hh.
References deltaEta(), and Jet::momentum().
| double Rivet::deltaEta | ( | const Vector3 & | v, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 400 of file Jet.hh.
References deltaEta(), and Jet::momentum().
00400 { 00401 return deltaEta(v, j.momentum()); 00402 }
| double Rivet::deltaEta | ( | const FourVector & | v, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 396 of file Jet.hh.
References deltaEta(), and Jet::momentum().
00396 { 00397 return deltaEta(v, j.momentum()); 00398 }
| double Rivet::deltaEta | ( | const FourMomentum & | v, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 392 of file Jet.hh.
References deltaEta(), and Jet::momentum().
00392 { 00393 return deltaEta(v, j.momentum()); 00394 }
| double Rivet::deltaEta | ( | const Jet & | j, | |
| double | eta | |||
| ) | [inline] |
Definition at line 388 of file Jet.hh.
References deltaEta(), and Jet::momentum().
| double Rivet::deltaEta | ( | const Jet & | j, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 384 of file Jet.hh.
References deltaEta(), and Jet::momentum().
00384 { 00385 return deltaEta(j.momentum(), v); 00386 }
| double Rivet::deltaEta | ( | const Jet & | j, | |
| const FourVector & | v | |||
| ) | [inline] |
Definition at line 380 of file Jet.hh.
References deltaEta(), and Jet::momentum().
00380 { 00381 return deltaEta(j.momentum(), v); 00382 }
| double Rivet::deltaEta | ( | const Jet & | j, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Definition at line 376 of file Jet.hh.
References deltaEta(), and Jet::momentum().
00376 { 00377 return deltaEta(j.momentum(), v); 00378 }
| double Rivet::deltaEta | ( | const Particle & | p, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 372 of file Jet.hh.
References deltaEta(), Jet::momentum(), and Particle::momentum().
00372 { 00373 return deltaEta(p.momentum(), j.momentum()); 00374 }
| double Rivet::deltaEta | ( | const Jet & | j, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 368 of file Jet.hh.
References deltaEta(), Particle::momentum(), and Jet::momentum().
00368 { 00369 return deltaEta(j.momentum(), p.momentum()); 00370 }
| double Rivet::deltaEta | ( | const Jet & | j1, | |
| const Jet & | j2 | |||
| ) | [inline] |
Definition at line 364 of file Jet.hh.
References Jet::momentum().
Referenced by deltaEta().
00364 { 00365 return deltaEta(j1.momentum(), j2.momentum()); 00366 }
| double Rivet::deltaPhi | ( | double | phi, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 275 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
| double Rivet::deltaPhi | ( | const Vector3 & | v, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 271 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
00271 { 00272 return deltaPhi(v, p.momentum()); 00273 }
| double Rivet::deltaPhi | ( | const FourVector & | v, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 267 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
00267 { 00268 return deltaPhi(v, p.momentum()); 00269 }
| double Rivet::deltaPhi | ( | const FourMomentum & | v, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 263 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
00263 { 00264 return deltaPhi(v, p.momentum()); 00265 }
| double Rivet::deltaPhi | ( | const Particle & | p, | |
| double | phi | |||
| ) | [inline] |
Definition at line 259 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
| double Rivet::deltaPhi | ( | const Particle & | p, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 255 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
00255 { 00256 return deltaPhi(p.momentum(), v); 00257 }
| double Rivet::deltaPhi | ( | const Particle & | p, | |
| const FourVector & | v | |||
| ) | [inline] |
Definition at line 251 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
00251 { 00252 return deltaPhi(p.momentum(), v); 00253 }
| double Rivet::deltaPhi | ( | const Particle & | p, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Definition at line 247 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
00247 { 00248 return deltaPhi(p.momentum(), v); 00249 }
| double Rivet::deltaPhi | ( | const Particle & | p1, | |
| const Particle & | p2 | |||
| ) | [inline] |
Definition at line 243 of file Particle.hh.
References deltaPhi(), and Particle::momentum().
00243 { 00244 return deltaPhi(p1.momentum(), p2.momentum()); 00245 }
| double Rivet::deltaPhi | ( | const Vector3 & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 848 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00848 { 00849 return deltaPhi(a, b.vector3()); 00850 }
| double Rivet::deltaPhi | ( | const FourMomentum & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 843 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00843 { 00844 return deltaPhi(a.vector3(), b); 00845 }
| double Rivet::deltaPhi | ( | const Vector3 & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 838 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00838 { 00839 return deltaPhi(a, b.vector3()); 00840 }
| double Rivet::deltaPhi | ( | const FourVector & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 833 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00833 { 00834 return deltaPhi(a.vector3(), b); 00835 }
| double Rivet::deltaPhi | ( | const FourMomentum & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 828 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00828 { 00829 return deltaPhi(a.vector3(), b.vector3()); 00830 }
| double Rivet::deltaPhi | ( | const FourVector & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 823 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00823 { 00824 return deltaPhi(a.vector3(), b.vector3()); 00825 }
| double Rivet::deltaPhi | ( | double | phi1, | |
| const FourVector & | v | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 818 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00818 { 00819 return deltaPhi(phi1, v.vector3()); 00820 }
| double Rivet::deltaPhi | ( | const FourVector & | v, | |
| double | phi2 | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 813 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00813 { 00814 return deltaPhi(v.vector3(), phi2); 00815 }
| double Rivet::deltaPhi | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 808 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00808 { 00809 return deltaPhi(a.vector3(), b.vector3()); 00810 }
| double Rivet::deltaPhi | ( | double | phi1, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 803 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00803 { 00804 return deltaPhi(phi1, v.vector3()); 00805 }
| double Rivet::deltaPhi | ( | const FourMomentum & | v, | |
| double | phi2 | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 798 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00798 { 00799 return deltaPhi(v.vector3(), phi2); 00800 }
| double Rivet::deltaPhi | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 793 of file Vector4.hh.
References deltaPhi(), and FourVector::vector3().
00793 { 00794 return deltaPhi(a.vector3(), b.vector3()); 00795 }
| double Rivet::deltaPhi | ( | double | phi1, | |
| const Vector3 & | v | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 366 of file Vector3.hh.
References Vector3::azimuthalAngle(), and deltaPhi().
00366 { 00367 return deltaPhi(phi1, v.azimuthalAngle()); 00368 }
| double Rivet::deltaPhi | ( | const Vector3 & | v, | |
| double | phi2 | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 361 of file Vector3.hh.
References Vector3::azimuthalAngle(), and deltaPhi().
00361 { 00362 return deltaPhi(v.azimuthalAngle(), phi2); 00363 }
| double Rivet::deltaPhi | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the difference in azimuthal angle between two spatial vectors.
Definition at line 356 of file Vector3.hh.
References Vector3::azimuthalAngle(), and deltaPhi().
00356 { 00357 return deltaPhi(a.azimuthalAngle(), b.azimuthalAngle()); 00358 }
| double Rivet::deltaPhi | ( | double | phi1, | |
| double | phi2 | |||
| ) | [inline] |
Calculate the difference between two angles in radians, returning in the range [0, PI].
Definition at line 388 of file MathUtils.hh.
References mapAngle0ToPi().
00388 { 00389 return mapAngle0ToPi(phi1 - phi2); 00390 }
| double Rivet::deltaPhi | ( | double | phi, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 359 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
| double Rivet::deltaPhi | ( | const Vector3 & | v, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 355 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
00355 { 00356 return deltaPhi(v, j.momentum()); 00357 }
| double Rivet::deltaPhi | ( | const FourVector & | v, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 351 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
00351 { 00352 return deltaPhi(v, j.momentum()); 00353 }
| double Rivet::deltaPhi | ( | const FourMomentum & | v, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 347 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
00347 { 00348 return deltaPhi(v, j.momentum()); 00349 }
| double Rivet::deltaPhi | ( | const Jet & | j, | |
| double | phi | |||
| ) | [inline] |
Definition at line 343 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
| double Rivet::deltaPhi | ( | const Jet & | j, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 339 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
00339 { 00340 return deltaPhi(j.momentum(), v); 00341 }
| double Rivet::deltaPhi | ( | const Jet & | j, | |
| const FourVector & | v | |||
| ) | [inline] |
Definition at line 335 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
00335 { 00336 return deltaPhi(j.momentum(), v); 00337 }
| double Rivet::deltaPhi | ( | const Jet & | j, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Definition at line 331 of file Jet.hh.
References deltaPhi(), and Jet::momentum().
00331 { 00332 return deltaPhi(j.momentum(), v); 00333 }
| double Rivet::deltaPhi | ( | const Particle & | p, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 327 of file Jet.hh.
References deltaPhi(), Jet::momentum(), and Particle::momentum().
00327 { 00328 return deltaPhi(p.momentum(), j.momentum()); 00329 }
| double Rivet::deltaPhi | ( | const Jet & | j, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 323 of file Jet.hh.
References deltaPhi(), Particle::momentum(), and Jet::momentum().
00323 { 00324 return deltaPhi(j.momentum(), p.momentum()); 00325 }
| double Rivet::deltaPhi | ( | const Jet & | j1, | |
| const Jet & | j2 | |||
| ) | [inline] |
Definition at line 319 of file Jet.hh.
References Jet::momentum().
Referenced by STAR_2009_UE_HELEN::analyze(), STAR_2008_S7993412::analyze(), MC_PHOTONJETUE::analyze(), MC_LEADINGJETS::analyze(), MC_DIPHOTON::analyze(), D0_2009_S8349509::analyze(), D0_2004_S5992206::analyze(), CDF_2010_S8591881_QCD::analyze(), CDF_2010_S8591881_DY::analyze(), CDF_2008_NOTE_9351::analyze(), CDF_2008_LEADINGJETS::analyze(), CDF_2001_S4751469::analyze(), CDF_1994_S2952106::analyze(), ATLAS_2011_S9002537::analyze(), ATLAS_2011_S8994773::analyze(), ATLAS_2011_S8983313::analyze(), ATLAS_2011_CONF_2011_090::analyze(), ATLAS_2010_S8894728::analyze(), deltaPhi(), and deltaR().
00319 { 00320 return deltaPhi(j1.momentum(), j2.momentum()); 00321 }
| double Rivet::deltaR | ( | double | eta, | |
| double | phi, | |||
| const Particle & | p | |||
| ) | [inline] |
Definition at line 238 of file Particle.hh.
References deltaR(), and Particle::momentum().
| double Rivet::deltaR | ( | const Vector3 & | v, | |
| const Particle & | p | |||
| ) | [inline] |
Definition at line 234 of file Particle.hh.
References deltaR(), and Particle::momentum().
00234 { 00235 return deltaR(v, p.momentum()); 00236 }
| double Rivet::deltaR | ( | const FourVector & | v, | |
| const Particle & | p, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 229 of file Particle.hh.
References deltaR(), and Particle::momentum().
00230 { 00231 return deltaR(v, p.momentum(), scheme); 00232 }
| double Rivet::deltaR | ( | const FourMomentum & | v, | |
| const Particle & | p, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 224 of file Particle.hh.
References deltaR(), and Particle::momentum().
00225 { 00226 return deltaR(v, p.momentum(), scheme); 00227 }
| double Rivet::deltaR | ( | const Particle & | p, | |
| double | eta, | |||
| double | phi | |||
| ) | [inline] |
Definition at line 220 of file Particle.hh.
References deltaR(), and Particle::momentum().
| double Rivet::deltaR | ( | const Particle & | p, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 216 of file Particle.hh.
References deltaR(), and Particle::momentum().
00216 { 00217 return deltaR(p.momentum(), v); 00218 }
| double Rivet::deltaR | ( | const Particle & | p, | |
| const FourVector & | v, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 211 of file Particle.hh.
References deltaR(), and Particle::momentum().
00212 { 00213 return deltaR(p.momentum(), v, scheme); 00214 }
| double Rivet::deltaR | ( | const Particle & | p, | |
| const FourMomentum & | v, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 206 of file Particle.hh.
References deltaR(), and Particle::momentum().
00207 { 00208 return deltaR(p.momentum(), v, scheme); 00209 }
| double Rivet::deltaR | ( | const Particle & | p1, | |
| const Particle & | p2, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 201 of file Particle.hh.
References deltaR(), and Particle::momentum().
00202 { 00203 return deltaR(p1.momentum(), p2.momentum(), scheme); 00204 }
| double Rivet::deltaR | ( | const Vector3 & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector.
Definition at line 783 of file Vector4.hh.
References deltaR(), and FourVector::vector3().
00783 { 00784 return deltaR(a, b.vector3()); 00785 }
| double Rivet::deltaR | ( | const FourVector & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector.
Definition at line 777 of file Vector4.hh.
References deltaR(), and FourVector::vector3().
00777 { 00778 return deltaR(a.vector3(), b); 00779 }
| double Rivet::deltaR | ( | const Vector3 & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector.
Definition at line 771 of file Vector4.hh.
References deltaR(), and FourVector::vector3().
00771 { 00772 return deltaR(a, b.vector3()); 00773 }
| double Rivet::deltaR | ( | const FourMomentum & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between a three-vector and a four-vector.
Definition at line 765 of file Vector4.hh.
References deltaR(), and FourVector::vector3().
00765 { 00766 return deltaR(a.vector3(), b); 00767 }
| double Rivet::deltaR | ( | const FourVector & | a, | |
| const FourMomentum & | b, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter.
Definition at line 751 of file Vector4.hh.
References FourVector::azimuthalAngle(), deltaR(), PSEUDORAPIDITY, FourMomentum::rapidity(), rapidity(), RAPIDITY, and FourVector::vector3().
00752 { 00753 switch (scheme) { 00754 case PSEUDORAPIDITY: 00755 return deltaR(a.vector3(), b.vector3()); 00756 case RAPIDITY: 00757 return deltaR(FourMomentum(a).rapidity(), a.azimuthalAngle(), b.rapidity(), b.azimuthalAngle()); 00758 default: 00759 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00760 } 00761 }
| double Rivet::deltaR | ( | const FourMomentum & | a, | |
| const FourVector & | b, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter.
Definition at line 734 of file Vector4.hh.
References FourVector::azimuthalAngle(), deltaR(), PSEUDORAPIDITY, FourMomentum::rapidity(), RAPIDITY, and FourVector::vector3().
00735 { 00736 switch (scheme) { 00737 case PSEUDORAPIDITY: 00738 return deltaR(a.vector3(), b.vector3()); 00739 case RAPIDITY: 00740 return deltaR(a.rapidity(), a.azimuthalAngle(), FourMomentum(b).rapidity(), b.azimuthalAngle()); 00741 default: 00742 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00743 } 00744 }
| double Rivet::deltaR | ( | double | eta1, | |
| double | phi1, | |||
| const FourMomentum & | v, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter.
Definition at line 716 of file Vector4.hh.
References FourVector::azimuthalAngle(), deltaR(), PSEUDORAPIDITY, FourMomentum::rapidity(), RAPIDITY, and FourVector::vector3().
00718 { 00719 switch (scheme) { 00720 case PSEUDORAPIDITY: 00721 return deltaR(eta1, phi1, v.vector3()); 00722 case RAPIDITY: 00723 return deltaR(eta1, phi1, v.rapidity(), v.azimuthalAngle()); 00724 default: 00725 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00726 } 00727 }
| double Rivet::deltaR | ( | const FourMomentum & | v, | |
| double | eta2, | |||
| double | phi2, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter.
Definition at line 697 of file Vector4.hh.
References FourVector::azimuthalAngle(), deltaR(), PSEUDORAPIDITY, FourMomentum::rapidity(), RAPIDITY, and FourVector::vector3().
00699 { 00700 switch (scheme) { 00701 case PSEUDORAPIDITY: 00702 return deltaR(v.vector3(), eta2, phi2); 00703 case RAPIDITY: 00704 return deltaR(v.rapidity(), v.azimuthalAngle(), eta2, phi2); 00705 default: 00706 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00707 } 00708 }
| double Rivet::deltaR | ( | const FourMomentum & | a, | |
| const FourMomentum & | b, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter.
Definition at line 680 of file Vector4.hh.
References FourVector::azimuthalAngle(), deltaR(), PSEUDORAPIDITY, FourMomentum::rapidity(), RAPIDITY, and FourVector::vector3().
00681 { 00682 switch (scheme) { 00683 case PSEUDORAPIDITY: 00684 return deltaR(a.vector3(), b.vector3()); 00685 case RAPIDITY: 00686 return deltaR(a.rapidity(), a.azimuthalAngle(), b.rapidity(), b.azimuthalAngle()); 00687 default: 00688 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00689 } 00690 }
| double Rivet::deltaR | ( | double | eta1, | |
| double | phi1, | |||
| const FourVector & | v, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter.
Definition at line 654 of file Vector4.hh.
References deltaR(), PSEUDORAPIDITY, RAPIDITY, and FourVector::vector3().
00656 { 00657 switch (scheme) { 00658 case PSEUDORAPIDITY : 00659 return deltaR(eta1, phi1, v.vector3()); 00660 case RAPIDITY: 00661 { 00662 const FourMomentum* mv = dynamic_cast<const FourMomentum*>(&v); 00663 if (!mv) { 00664 string err = "deltaR with scheme RAPIDITY can only be called with FourMomentum objects, not FourVectors"; 00665 throw std::runtime_error(err); 00666 } 00667 return deltaR(eta1, phi1, *mv, scheme); 00668 } 00669 default: 00670 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00671 } 00672 }
| double Rivet::deltaR | ( | const FourVector & | v, | |
| double | eta2, | |||
| double | phi2, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter.
Definition at line 628 of file Vector4.hh.
References deltaR(), PSEUDORAPIDITY, RAPIDITY, and FourVector::vector3().
00630 { 00631 switch (scheme) { 00632 case PSEUDORAPIDITY : 00633 return deltaR(v.vector3(), eta2, phi2); 00634 case RAPIDITY: 00635 { 00636 const FourMomentum* mv = dynamic_cast<const FourMomentum*>(&v); 00637 if (!mv) { 00638 string err = "deltaR with scheme RAPIDITY can only be called with FourMomentum objects, not FourVectors"; 00639 throw std::runtime_error(err); 00640 } 00641 return deltaR(*mv, eta2, phi2, scheme); 00642 } 00643 default: 00644 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00645 } 00646 }
| double Rivet::deltaR | ( | const FourVector & | a, | |
| const FourVector & | b, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two four-vectors. There is a scheme ambiguity for momentum-type four vectors as to whether the pseudorapidity (a purely geometric concept) or the rapidity (a relativistic energy-momentum quantity) is to be used: this can be chosen via the optional scheme parameter. Use of this scheme option is discouraged in this case since RAPIDITY is only a valid option for vectors whose type is really the FourMomentum derived class.
Definition at line 602 of file Vector4.hh.
References deltaR(), PSEUDORAPIDITY, RAPIDITY, and FourVector::vector3().
00603 { 00604 switch (scheme) { 00605 case PSEUDORAPIDITY : 00606 return deltaR(a.vector3(), b.vector3()); 00607 case RAPIDITY: 00608 { 00609 const FourMomentum* ma = dynamic_cast<const FourMomentum*>(&a); 00610 const FourMomentum* mb = dynamic_cast<const FourMomentum*>(&b); 00611 if (!ma || !mb) { 00612 string err = "deltaR with scheme RAPIDITY can only be called with FourMomentum objects, not FourVectors"; 00613 throw std::runtime_error(err); 00614 } 00615 return deltaR(*ma, *mb, scheme); 00616 } 00617 default: 00618 throw std::runtime_error("The specified deltaR scheme is not yet implemented"); 00619 } 00620 }
| double Rivet::deltaR | ( | double | eta1, | |
| double | phi1, | |||
| const Vector3 & | v | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two spatial vectors.
Definition at line 388 of file Vector3.hh.
References Vector3::azimuthalAngle(), deltaR(), and Vector3::pseudorapidity().
00388 { 00389 return deltaR(eta1, phi1, v.pseudorapidity(), v.azimuthalAngle()); 00390 }
| double Rivet::deltaR | ( | const Vector3 & | v, | |
| double | eta2, | |||
| double | phi2 | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two spatial vectors.
Definition at line 383 of file Vector3.hh.
References Vector3::azimuthalAngle(), deltaR(), and Vector3::pseudorapidity().
00383 { 00384 return deltaR(v.pseudorapidity(), v.azimuthalAngle(), eta2, phi2); 00385 }
| double Rivet::deltaR | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Calculate the 2D rapidity-azimuthal ("eta-phi") distance between two spatial vectors.
Definition at line 377 of file Vector3.hh.
References Vector3::azimuthalAngle(), deltaR(), and Vector3::pseudorapidity().
00377 { 00378 return deltaR(a.pseudorapidity(), a.azimuthalAngle(), 00379 b.pseudorapidity(), b.azimuthalAngle()); 00380 }
| double Rivet::deltaR | ( | double | rap1, | |
| double | phi1, | |||
| double | rap2, | |||
| double | phi2 | |||
| ) | [inline] |
Calculate the distance between two points in 2D rapidity-azimuthal ("\f$ \eta-\phi \f$") space. The phi values are given in radians.
Definition at line 400 of file MathUtils.hh.
References deltaPhi(), and sqr().
| double Rivet::deltaR | ( | double | eta, | |
| double | phi, | |||
| const Jet & | j | |||
| ) | [inline] |
| double Rivet::deltaR | ( | const Vector3 & | v, | |
| const Jet & | j | |||
| ) | [inline] |
Definition at line 310 of file Jet.hh.
References deltaR(), and Jet::momentum().
00310 { 00311 return deltaR(v, j.momentum()); 00312 }
| double Rivet::deltaR | ( | const FourVector & | v, | |
| const Jet & | j, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 305 of file Jet.hh.
References deltaR(), and Jet::momentum().
00306 { 00307 return deltaR(v, j.momentum(), scheme); 00308 }
| double Rivet::deltaR | ( | const FourMomentum & | v, | |
| const Jet & | j, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 300 of file Jet.hh.
References deltaR(), and Jet::momentum().
00301 { 00302 return deltaR(v, j.momentum(), scheme); 00303 }
| double Rivet::deltaR | ( | const Jet & | j, | |
| double | eta, | |||
| double | phi | |||
| ) | [inline] |
| double Rivet::deltaR | ( | const Jet & | j, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 292 of file Jet.hh.
References deltaR(), and Jet::momentum().
00292 { 00293 return deltaR(j.momentum(), v); 00294 }
| double Rivet::deltaR | ( | const Jet & | j, | |
| const FourVector & | v, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 287 of file Jet.hh.
References deltaR(), and Jet::momentum().
00288 { 00289 return deltaR(j.momentum(), v, scheme); 00290 }
| double Rivet::deltaR | ( | const Jet & | j, | |
| const FourMomentum & | v, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 282 of file Jet.hh.
References deltaR(), and Jet::momentum().
00283 { 00284 return deltaR(j.momentum(), v, scheme); 00285 }
| double Rivet::deltaR | ( | const Particle & | p, | |
| const Jet & | j, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 277 of file Jet.hh.
References deltaR(), Jet::momentum(), and Particle::momentum().
00278 { 00279 return deltaR(p.momentum(), j.momentum(), scheme); 00280 }
| double Rivet::deltaR | ( | const Jet & | j, | |
| const Particle & | p, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 272 of file Jet.hh.
References deltaR(), Particle::momentum(), and Jet::momentum().
00273 { 00274 return deltaR(j.momentum(), p.momentum(), scheme); 00275 }
| double Rivet::deltaR | ( | const Jet & | j1, | |
| const Jet & | j2, | |||
| RapScheme | scheme = PSEUDORAPIDITY | |||
| ) | [inline] |
Definition at line 267 of file Jet.hh.
References Jet::momentum().
Referenced by CDF_2004_S5839831::_calcTransCones(), MC_ZZJETS::analyze(), MC_ZJETS::analyze(), MC_WWJETS::analyze(), MC_WJETS::analyze(), MC_SUSY::analyze(), MC_PHOTONJETUE::analyze(), MC_PHOTONJETS::analyze(), MC_JetAnalysis::analyze(), MC_HJETS::analyze(), MC_DIPHOTON::analyze(), D0_2010_S8570965::analyze(), D0_2008_S7719523::analyze(), D0_2008_S6879055::analyze(), D0_2006_S6438750::analyze(), D0_1996_S3214044::analyze(), CDF_2009_S8436959::analyze(), CDF_2008_S8095620::analyze(), CDF_2008_S7540469::analyze(), CDF_2006_S6653332::analyze(), CDF_2005_S6080774::analyze(), CDF_2004_S5839831::analyze(), CDF_1997_S3541940::analyze(), CDF_1996_S3349578::analyze(), CDF_1994_S2952106::analyze(), CDF_1993_S2742446::analyze(), ATLAS_2011_S9120807::analyze(), ATLAS_2011_S9019561::analyze(), ATLAS_2011_S9002537::analyze(), ATLAS_2011_S8983313::analyze(), ATLAS_2011_CONF_2011_090::analyze(), ATLAS_2010_S8919674::analyze(), ATLAS_2010_S8914702::analyze(), JetShape::calc(), deltaR(), SVertex::project(), LeptonClusters::project(), and ClusteredPhotons::project().
00268 { 00269 return deltaR(j1.momentum(), j2.momentum(), scheme); 00270 }
| double Rivet::det | ( | const Matrix< N > & | m | ) | [inline] |
Definition at line 353 of file MatrixN.hh.
00353 { 00354 return m.determinant(); 00355 }
| EigenSystem< N > diagonalize | ( | const Matrix< N > & | m | ) | [inline] |
Diagonalize an NxN matrix, returning a collection of pairs of eigenvalues and eigenvectors, ordered decreasing in eigenvalue.
Definition at line 112 of file MatrixDiag.hh.
References EigenSystem< N >::_eigenPairs, Rivet::PID::A(), Matrix< N >::get(), and Vector< N >::set().
Referenced by FParameter::_calcFParameter(), and Sphericity::_calcSphericity().
00112 { 00113 EigenSystem<N> esys; 00114 00115 // Make a GSL matrix. 00116 gsl_matrix* A = gsl_matrix_alloc(N, N); 00117 for (size_t i = 0; i < N; ++i) { 00118 for (size_t j = 0; j < N; ++j) { 00119 gsl_matrix_set(A, i, j, m.get(i, j)); 00120 } 00121 } 00122 00123 // Use GSL diagonalization. 00124 gsl_matrix* vecs = gsl_matrix_alloc(N, N); 00125 gsl_vector* vals = gsl_vector_alloc(N); 00126 gsl_eigen_symmv_workspace* workspace = gsl_eigen_symmv_alloc(N); 00127 gsl_eigen_symmv(A, vals, vecs, workspace); 00128 gsl_eigen_symmv_sort(vals, vecs, GSL_EIGEN_SORT_VAL_DESC); 00129 00130 // Build the vector of "eigen-pairs". 00131 typename EigenSystem<N>::EigenPairs eigensolns; 00132 for (size_t i = 0; i < N; ++i) { 00133 typename EigenSystem<N>::EigenPair ep; 00134 ep.first = gsl_vector_get(vals, i); 00135 Vector<N> ev; 00136 for (size_t j = 0; j < N; ++j) { 00137 ev.set(j, gsl_matrix_get(vecs, j, i)); 00138 } 00139 ep.second = ev; 00140 eigensolns.push_back(ep); 00141 } 00142 00143 // Free GSL memory. 00144 gsl_eigen_symmv_free(workspace); 00145 gsl_matrix_free(A); 00146 gsl_matrix_free(vecs); 00147 gsl_vector_free(vals); 00148 00149 // Populate the returned object. 00150 esys._eigenPairs = eigensolns; 00151 return esys; 00152 }
| Matrix< N > divide | ( | const Matrix< N > & | m, | |
| const double | a | |||
| ) | [inline] |
Definition at line 296 of file MatrixN.hh.
References multiply().
| double Rivet::dot | ( | const Vector< 2 > & | a, | |
| const Vector< 2 > & | b | |||
| ) | [inline] |
Definition at line 49 of file Spherocity.cc.
| double Rivet::dot | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Contract two 4-vectors, with metric signature (+ - - -).
Definition at line 199 of file Vector4.hh.
References contract().
00199 { 00200 return contract(a, b); 00201 }
| double Rivet::dot | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Definition at line 216 of file Vector3.hh.
References Vector3::dot().
Referenced by Thrust::_calcThrust(), D0_1996_S3214044::_fourJetAnalysis(), DELPHI_1996_S3430090::analyze(), ALEPH_2004_S5765862::analyze(), ALEPH_1996_S3486095::analyze(), Hemispheres::project(), and DISKinematics::project().
| bool Rivet::endsWith | ( | const string & | s, | |
| const string & | end | |||
| ) | [inline] |
| double Rivet::Et | ( | const FourMomentum & | v | ) | [inline] |
Calculate the transverse energy 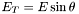 of a momentum 4-vector.
of a momentum 4-vector.
Definition at line 579 of file Vector4.hh.
References FourMomentum::Et().
Referenced by H1_2000_S4129130::analyze(), H1_1994_S2919893::analyze(), CDF_1997_S3541940::analyze(), CDF_1996_S3349578::analyze(), and CDF_1996_S3108457::analyze().
| double Rivet::Et2 | ( | const FourMomentum & | v | ) | [inline] |
Calculate the transverse energy squared, 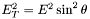 of a momentum 4-vector.
of a momentum 4-vector.
Definition at line 575 of file Vector4.hh.
References FourMomentum::Et2().
| double Rivet::eta | ( | const FourVector & | v | ) | [inline] |
Synonym for pseudorapidity.
Definition at line 310 of file Vector4.hh.
References FourVector::eta().
| double Rivet::eta | ( | const Vector3 & | v | ) | [inline] |
Synonym for pseudorapidity.
Definition at line 324 of file Vector3.hh.
References Vector3::eta().
Referenced by FinalState::accept(), UA5_1986_S1583476::analyze(), UA5_1982_S875503::analyze(), UA1_1990_S2044935::analyze(), SFM_1984_S1178091::analyze(), MC_GENERIC::analyze(), H1_2000_S4129130::analyze(), H1_1994_S2919893::analyze(), D0_1996_S3324664::analyze(), CMS_2011_S8957746::analyze(), CMS_2011_S8884919::analyze(), CMS_2010_S8656010::analyze(), CMS_2010_S8547297::analyze(), CDF_2010_S8591881_QCD::analyze(), CDF_2008_LEADINGJETS::analyze(), CDF_2001_S4563131::analyze(), CDF_1997_S3541940::analyze(), CDF_1990_S2089246::analyze(), ATLAS_2011_S9120807::analyze(), ATLAS_2010_S8914702::analyze(), ALICE_2010_S8625980::analyze(), ATLAS_2011_S9120807::getEtaBin(), ATLAS_2010_S8914702::getEtaBin(), TriggerUA5::project(), TriggerCDFRun2::project(), TriggerCDFRun0Run1::project(), and InitialQuarks::project().
| string findAnalysisInfoFile | ( | const std::string & | filename, | |
| const std::vector< std::string > & | pathprepend = std::vector<std::string>(), |
|||
| const std::vector< std::string > & | pathappend = std::vector<std::string>() | |||
| ) |
Find the first file of the given name in the analysis info file search dirs.
- Note:
- If none found, returns an empty string
Definition at line 112 of file RivetPaths.cc.
Referenced by AnalysisInfo::make().
00115 { 00116 const vector<string> paths = pathprepend + getAnalysisInfoPaths() + pathappend;
| string findAnalysisLibFile | ( | const std::string & | filename | ) |
Find the first file of the given name in the analysis library search dirs.
- Note:
- If none found, returns an empty string
Definition at line 70 of file RivetPaths.cc.
| string findAnalysisPlotFile | ( | const std::string & | filename, | |
| const std::vector< std::string > & | pathprepend = std::vector<std::string>(), |
|||
| const std::vector< std::string > & | pathappend = std::vector<std::string>() | |||
| ) |
Find the first file of the given name in the analysis plot file search dirs.
- Note:
- If none found, returns an empty string
Definition at line 134 of file RivetPaths.cc.
00137 { 00138 const vector<string> paths = pathprepend + getAnalysisPlotPaths() + pathappend;
| string findAnalysisRefFile | ( | const std::string & | filename, | |
| const std::vector< std::string > & | pathprepend = std::vector<std::string>(), |
|||
| const std::vector< std::string > & | pathappend = std::vector<std::string>() | |||
| ) |
Find the first file of the given name in the ref data file search dirs.
- Note:
- If none found, returns an empty string
Definition at line 90 of file RivetPaths.cc.
Referenced by getDatafilePath().
00093 { 00094 const vector<string> paths = pathprepend + getAnalysisRefPaths() + pathappend;
| bool Rivet::fuzzyEquals | ( | const Vector< N > & | va, | |
| const Vector< N > & | vb, | |||
| double | tolerance = 1E-5 | |||
| ) | [inline] |
Compare two vectors by index, allowing for numerical precision.
Definition at line 189 of file VectorN.hh.
References fuzzyEquals(), and Vector< N >::get().
00189 { 00190 for (size_t i = 0; i < N; ++i) { 00191 const double a = va.get(i); 00192 const double b = vb.get(i); 00193 if (!Rivet::fuzzyEquals(a, b, tolerance)) return false; 00194 } 00195 return true; 00196 }
| bool Rivet::fuzzyEquals | ( | const Matrix< N > & | ma, | |
| const Matrix< N > & | mb, | |||
| double | tolerance = 1E-5 | |||
| ) | [inline] |
Compare two matrices by index, allowing for numerical precision.
Definition at line 397 of file MatrixN.hh.
References fuzzyEquals(), and Matrix< N >::get().
00397 { 00398 for (size_t i = 0; i < N; ++i) { 00399 for (size_t j = 0; j < N; ++j) { 00400 const double a = ma.get(i, j); 00401 const double b = mb.get(i, j); 00402 if (!Rivet::fuzzyEquals(a, b, tolerance)) return false; 00403 } 00404 } 00405 return true; 00406 }
| bool Rivet::fuzzyEquals | ( | long | a, | |
| long | b, | |||
| double | UNUSEDtolerance = 1E-5 | |||
| ) | [inline] |
Compare two integral-type numbers for equality with a degree of fuzziness. Since there is no risk of floating point error with integral types, this function just exists in case fuzzyEquals is accidentally used on an integer type, to avoid implicit type conversion. The tolerance parameter is ignored, even if it would have an absolute magnitude greater than 1.
Definition at line 45 of file MathUtils.hh.
| bool Rivet::fuzzyEquals | ( | double | a, | |
| double | b, | |||
| double | tolerance = 1E-5 | |||
| ) | [inline] |
Compare two floating point numbers for equality with a degree of fuzziness The tolerance parameter is fractional.
Definition at line 32 of file MathUtils.hh.
Referenced by Sphericity::_calcSphericity(), Cmp< double >::_compare(), UA1_1990_S2044935::analyze(), CDF_2004_S5839831::analyze(), ATLAS_2010_S8918562::analyze(), ATLAS_2010_S8894728::analyze(), AnalysisHandler::analyze(), ALICE_2010_S8625980::analyze(), ALEPH_2004_S5765862::analyze(), Sphericity::compare(), UA1_1990_S2044935::finalize(), CMS_2011_S8978280::finalize(), CDF_2004_S5839831::finalize(), CDF_2002_S4796047::finalize(), ATLAS_2010_S8918562::finalize(), ALICE_2010_S8625980::finalize(), ALEPH_2004_S5765862::finalize(), fuzzyEquals(), fuzzyGtrEquals(), fuzzyLessEquals(), getBinEdges(), OPAL_2004_S6132243::getHistIndex(), UA5_1989_S1926373::init(), UA5_1988_S1867512::init(), UA5_1986_S1583476::init(), UA1_1990_S2044935::init(), SFM_1984_S1178091::init(), CMS_2011_S8978280::init(), CMS_2011_S8884919::init(), CMS_2010_S8547297::init(), CDF_2004_S5839831::init(), CDF_2002_S4796047::init(), CDF_1990_S2089246::init(), CDF_1988_S1865951::init(), ATLAS_2011_S8994773::init(), ATLAS_2010_S8918562::init(), ATLAS_2010_S8894728::init(), ALICE_2010_S8625980::init(), ALICE_2010_S8624100::init(), inRange(), ALEPH_1996_S3196992::particleInJet(), and Run::readEvent().
| bool Rivet::fuzzyGtrEquals | ( | long | a, | |
| long | b, | |||
| double | UNUSEDtolerance = 1E-5 | |||
| ) | [inline] |
Compare two integral-type numbers for >= with a degree of fuzziness. Since there is no risk of floating point error with integral types, this function just exists in case fuzzyGtrEquals is accidentally used on an integer type, to avoid implicit type conversion. The tolerance parameter is ignored, even if it would have an absolute magnitude greater than 1.
Definition at line 62 of file MathUtils.hh.
| bool Rivet::fuzzyGtrEquals | ( | double | a, | |
| double | b, | |||
| double | tolerance = 1E-5 | |||
| ) | [inline] |
Compare two floating point numbers for >= with a degree of fuzziness The tolerance parameter on the equality test is as for fuzzyEquals.
Definition at line 52 of file MathUtils.hh.
References fuzzyEquals().
00052 { 00053 return a > b || fuzzyEquals(a, b, tolerance); 00054 }
| bool Rivet::fuzzyLessEquals | ( | long | a, | |
| long | b, | |||
| double | UNUSEDtolerance = 1E-5 | |||
| ) | [inline] |
Compare two integral-type numbers for <= with a degree of fuzziness. Since there is no risk of floating point error with integral types, this function just exists in case fuzzyLessEquals is accidentally used on an integer type, to avoid implicit type conversion. The tolerance parameter is ignored, even if it would have an absolute magnitude greater than 1.
Definition at line 79 of file MathUtils.hh.
| bool Rivet::fuzzyLessEquals | ( | double | a, | |
| double | b, | |||
| double | tolerance = 1E-5 | |||
| ) | [inline] |
Compare two floating point numbers for <= with a degree of fuzziness The tolerance parameter on the equality test is as for fuzzyEquals.
Definition at line 69 of file MathUtils.hh.
References fuzzyEquals().
00069 { 00070 return a < b || fuzzyEquals(a, b, tolerance); 00071 }
| double Rivet::get2dClosestApproach | ( | const HepMC::GenParticle & | track, | |
| const Vector3 & | vtx3pos | |||
| ) | [inline] |
- Todo:
- Whoa! - implicit constructors from hell!
Definition at line 14 of file SVertex.cc.
References sqr(), Vector3::x(), Vector3::y(), and Vector3::z().
Referenced by SVertex::_applyVtxTrackCuts().
00014 { 00015 /// @todo Whoa! - implicit constructors from hell! 00016 HepMC::FourVector trkvec = track; 00017 HepMC::ThreeVector trk3vec = trkvec; 00018 HepMC::ThreeVector trk3pos = track.production_vertex()->position(); 00019 00020 Vector3 diff(vtx3pos.x()-trk3pos.x(), vtx3pos.y()-trk3pos.y(), vtx3pos.z()-trk3pos.z()); 00021 00022 // Impact parameter in the transverse plane 00023 const double d = fabs( trk3vec.x()*diff.y() - trk3vec.y()*diff.x() ) 00024 / sqrt( sqr(trk3vec.x()) + sqr(trk3vec.y()) ); 00025 return d; 00026 }
| double Rivet::get2dDecayLength | ( | const Vector3 & | vtx1, | |
| const Vector3 & | vtx2, | |||
| const FourMomentum & | jetaxis | |||
| ) | [inline] |
Return Decay Length Significance between two vertices in transverse plane.
Definition at line 47 of file SVertex.cc.
References FourMomentum::px(), FourMomentum::py(), sqr(), Vector3::x(), and Vector3::y().
Referenced by SVertex::project().
| double Rivet::get3dClosestApproach | ( | const HepMC::GenParticle & | track, | |
| const Vector3 & | vtx3pos | |||
| ) | [inline] |
Definition at line 30 of file SVertex.cc.
References sqr(), Vector3::x(), Vector3::y(), and Vector3::z().
00030 { 00031 HepMC::FourVector trkvec = track; 00032 HepMC::ThreeVector trk3vec = trkvec; 00033 HepMC::FourVector trkpos = track.production_vertex()->position(); 00034 HepMC::ThreeVector trk3pos = trkpos; 00035 Vector3 diff(vtx3pos.x()-trk3pos.x(), vtx3pos.y()-trk3pos.y(), vtx3pos.z()-trk3pos.z()); 00036 00037 // Impact parameter in 3 dimensions 00038 const double mag = sqrt( sqr(trk3vec.x()) + sqr(trk3vec.y()) + sqr(trk3vec.z()) ); 00039 const double d = sqrt( sqr(trk3vec.y()*diff.z()-trk3vec.z()*diff.y()) - 00040 sqr(trk3vec.x()*diff.z()-trk3vec.z()*diff.x()) + 00041 sqr(trk3vec.x()*diff.y()-trk3vec.y()*diff.x()) ) / mag; 00042 return d; 00043 }
| double Rivet::get3dDecayLength | ( | const Vector3 & | vtx1, | |
| const Vector3 & | vtx2, | |||
| const FourMomentum & | jetaxis | |||
| ) | [inline] |
Return 3 dimensional Decay Length Significance between vertices.
Definition at line 57 of file SVertex.cc.
References FourMomentum::px(), FourMomentum::py(), FourMomentum::pz(), sqr(), Vector3::x(), Vector3::y(), and Vector3::z().
| vector< string > getAnalysisInfoPaths | ( | ) |
Get Rivet analysis info metadata search paths.
Definition at line 97 of file RivetPaths.cc.
References getAnalysisLibPaths(), getRivetDataPath(), and pathsplit().
00099 { 00100 vector<string> dirs; 00101 char* env = 0; 00102 env = getenv("RIVET_INFO_PATH"); 00103 if (env) { 00104 // Use the Rivet analysis path variable if set... 00105 dirs += pathsplit(env); 00106 } 00107 // Then fall back to the Rivet data install path... 00108 dirs += getRivetDataPath(); 00109 // ... and also add any analysis plugin search dirs for convenience 00110 dirs += getAnalysisLibPaths();
| vector< string > getAnalysisLibPaths | ( | ) |
Get Rivet analysis plugin library search paths.
Definition at line 57 of file RivetPaths.cc.
Referenced by AnalysisLoader::_loadAnalysisPlugins(), getAnalysisInfoPaths(), getAnalysisPlotPaths(), and getAnalysisRefPaths().
00059 { 00060 vector<string> dirs; 00061 char* env = 0; 00062 env = getenv("RIVET_ANALYSIS_PATH"); 00063 if (env) { 00064 // Use the Rivet analysis path variable if set... 00065 dirs += pathsplit(env); 00066 } 00067 // ... otherwise fall back to the Rivet library install path 00068 dirs += getLibPath();
| vector< string > getAnalysisPlotPaths | ( | ) |
Get Rivet analysis plot style search paths.
Definition at line 119 of file RivetPaths.cc.
References getAnalysisLibPaths(), getRivetDataPath(), and pathsplit().
00121 { 00122 vector<string> dirs; 00123 char* env = 0; 00124 env = getenv("RIVET_PLOT_PATH"); 00125 if (env) { 00126 // Use the Rivet analysis path variable if set... 00127 dirs += pathsplit(env); 00128 } 00129 // Then fall back to the Rivet data install path... 00130 dirs += getRivetDataPath(); 00131 // ... and also add any analysis plugin search dirs for convenience 00132 dirs += getAnalysisLibPaths();
| vector< string > getAnalysisRefPaths | ( | ) |
Get Rivet analysis reference data search paths.
Definition at line 75 of file RivetPaths.cc.
References getAnalysisLibPaths(), getRivetDataPath(), and pathsplit().
00077 { 00078 vector<string> dirs; 00079 char* env = 0; 00080 env = getenv("RIVET_REF_PATH"); 00081 if (env) { 00082 // Use the Rivet analysis path variable if set... 00083 dirs += pathsplit(env); 00084 } 00085 // Then fall back to the Rivet data install path... 00086 dirs += getRivetDataPath(); 00087 // ... and also add any analysis plugin search dirs for convenience 00088 dirs += getAnalysisLibPaths();
| map< string, BinEdges > getBinEdges | ( | const map< string, vector< DPSXPoint > > & | xpoints | ) |
Definition at line 194 of file RivetAIDA.cc.
References DPSXPoint::errminus, DPSXPoint::errplus, fuzzyEquals(), and DPSXPoint::val.
00194 { 00195 00196 map<string, BinEdges> rtn; 00197 for (map<string, vector<DPSXPoint> >::const_iterator dsit = xpoints.begin(); dsit != xpoints.end(); ++dsit) { 00198 const string plotname = dsit->first; 00199 list<double> edges; 00200 foreach (const DPSXPoint& xpt, dsit->second) { 00201 const double lowedge = xpt.val - xpt.errminus; 00202 const double highedge = xpt.val + xpt.errplus; 00203 edges.push_back(lowedge); 00204 edges.push_back(highedge); 00205 } 00206 00207 //cout << "*** " << edges << endl; 00208 00209 // Remove duplicates (the careful testing is why we haven't used a set) 00210 //cout << edges.size() << " edges -> " << edges.size()/2 << " bins" << endl; 00211 for (list<double>::iterator e = edges.begin(); e != edges.end(); ++e) { 00212 list<double>::iterator e2 = e; 00213 while (e2 != edges.end()) { 00214 if (e != e2) { 00215 if (fuzzyEquals(*e, *e2)) { 00216 edges.erase(e2++); 00217 } 00218 } 00219 ++e2; 00220 } 00221 } 00222 //cout << edges.size() << " edges after dups removal (should be #bins+1)" << endl; 00223 //cout << "@@@ " << edges << endl; 00224 00225 // Add to the map 00226 rtn[plotname] = BinEdges(edges.begin(), edges.end()); 00227 } 00228 00229 // Return 00230 return rtn; 00231 }
| map< string, BinEdges > getBinEdges | ( | string | papername | ) |
Function to get a map of all the bin edge vectors in a paper with the given papername.
Definition at line 187 of file RivetAIDA.cc.
References getDPSXValsErrs().
Referenced by Analysis::_cacheBinEdges().
00187 { 00188 const map<string, vector<DPSXPoint> > xpoints = getDPSXValsErrs(papername); 00189 return getBinEdges(xpoints); 00190 }
| string getDatafilePath | ( | string | papername | ) |
Get the file system path to the AIDA reference file for this paper.
Definition at line 21 of file RivetAIDA.cc.
References findAnalysisRefFile(), and getRivetDataPath().
Referenced by getDPSXValsErrs(), and getDPSXYValsErrs().
00021 { 00022 const string path = findAnalysisRefFile(papername + ".aida"); 00023 if (!path.empty()) return path; 00024 throw Rivet::Error("Couldn't find ref data file '" + papername + ".aida" + 00025 " in $RIVET_REF_PATH, " + getRivetDataPath() + ", or ."); 00026 return ""; 00027 }
| string getDataPath | ( | ) |
Get data install path.
Definition at line 31 of file RivetPaths.cc.
| map< string, vector< DPSXPoint > > getDPSXValsErrs | ( | string | papername | ) |
Check path to make sure that this is a reference histogram.
- Todo:
- Check that "path" matches filename
- Todo:
- Throw an exception here?
- Todo:
- Rethrow as a general XML failure.
Check path to make sure that this is a reference histogram.
- Todo:
- Check that "path" matches filename
- Todo:
- Throw an exception here?
- Todo:
- Rethrow as a general XML failure.
Definition at line 112 of file RivetAIDA.cc.
References getDatafilePath().
Referenced by Analysis::_cacheXAxisData(), and getBinEdges().
00112 { 00113 // Get filename 00114 const string xmlfile = getDatafilePath(papername); 00115 00116 // Open AIDA XML file 00117 TiXmlDocument doc(xmlfile); 00118 doc.LoadFile(); 00119 if (doc.Error()) { 00120 string err = "Error in " + string(doc.Value()); 00121 err += ": " + string(doc.ErrorDesc()); 00122 cerr << err << endl; 00123 throw Error(err); 00124 } 00125 00126 // Return value, to be populated 00127 map<string, vector<DPSXPoint> > rtn; 00128 00129 try { 00130 // Walk down tree to get to the <paper> element 00131 const TiXmlNode* aidaN = doc.FirstChild("aida"); 00132 if (!aidaN) throw Error("Couldn't get <aida> root element"); 00133 for (const TiXmlNode* dpsN = aidaN->FirstChild("dataPointSet"); dpsN; dpsN = dpsN->NextSibling()) { 00134 const TiXmlElement* dpsE = dpsN->ToElement(); 00135 const string plotname = dpsE->Attribute("name"); 00136 const string plotpath = dpsE->Attribute("path"); 00137 /// Check path to make sure that this is a reference histogram. 00138 if (plotpath.find("/REF") != 0) { 00139 cerr << "Skipping non-reference histogram " << plotname << endl; 00140 continue; 00141 } 00142 00143 /// @todo Check that "path" matches filename 00144 vector<DPSXPoint> points; 00145 for (const TiXmlNode* dpN = dpsN->FirstChild("dataPoint"); dpN; dpN = dpN->NextSibling()) { 00146 const TiXmlNode* xMeasN = dpN->FirstChild("measurement"); 00147 if (xMeasN) { 00148 const TiXmlElement* xMeasE = xMeasN->ToElement(); 00149 const string centreStr = xMeasE->Attribute("value"); 00150 const string errplusStr = xMeasE->Attribute("errorPlus"); 00151 const string errminusStr = xMeasE->Attribute("errorMinus"); 00152 //if (!centreStr) throw Error("Couldn't get a valid bin centre"); 00153 //if (!errplusStr) throw Error("Couldn't get a valid bin err+"); 00154 //if (!errminusStr) throw Error("Couldn't get a valid bin err-"); 00155 istringstream ssC(centreStr); 00156 istringstream ssP(errplusStr); 00157 istringstream ssM(errminusStr); 00158 double centre, errplus, errminus; 00159 ssC >> centre; ssP >> errplus; ssM >> errminus; 00160 //cout << " " << centre << " + " << errplus << " - " << errminus << endl; 00161 DPSXPoint pt(centre, errminus, errplus); 00162 points.push_back(pt); 00163 } else { 00164 cerr << "Couldn't get <measurement> tag" << endl; 00165 /// @todo Throw an exception here? 00166 } 00167 } 00168 00169 // Add to the map 00170 rtn[plotname] = points; 00171 } 00172 00173 } 00174 // Write out the error 00175 /// @todo Rethrow as a general XML failure. 00176 catch (std::exception& e) { 00177 cerr << e.what() << endl; 00178 throw; 00179 } 00180 00181 // Return 00182 return rtn; 00183 }
| map< string, vector< DPSXYPoint > > getDPSXYValsErrs | ( | string | papername | ) |
Check path to make sure that this is a reference histogram.
- Todo:
- Check that "path" matches filename
- Todo:
- Throw an exception here?
- Todo:
- Rethrow as a general XML failure.
Check path to make sure that this is a reference histogram.
- Todo:
- Check that "path" matches filename
- Todo:
- Throw an exception here?
- Todo:
- Rethrow as a general XML failure.
Definition at line 30 of file RivetAIDA.cc.
References getDatafilePath().
00030 { 00031 // Get filename 00032 const string xmlfile = getDatafilePath(papername); 00033 00034 // Open AIDA XML file 00035 TiXmlDocument doc(xmlfile); 00036 doc.LoadFile(); 00037 if (doc.Error()) { 00038 string err = "Error in " + string(doc.Value()); 00039 err += ": " + string(doc.ErrorDesc()); 00040 cerr << err << endl; 00041 throw Error(err); 00042 } 00043 00044 // Return value, to be populated 00045 map<string, vector<DPSXYPoint> > rtn; 00046 00047 try { 00048 // Walk down tree to get to the <paper> element 00049 const TiXmlNode* aidaN = doc.FirstChild("aida"); 00050 if (!aidaN) throw Error("Couldn't get <aida> root element"); 00051 for (const TiXmlNode* dpsN = aidaN->FirstChild("dataPointSet"); dpsN; dpsN = dpsN->NextSibling()) { 00052 const TiXmlElement* dpsE = dpsN->ToElement(); 00053 const string plotname = dpsE->Attribute("name"); 00054 const string plotpath = dpsE->Attribute("path"); 00055 /// Check path to make sure that this is a reference histogram. 00056 if (plotpath.find("/REF") != 0) { 00057 cerr << "Skipping non-reference histogram " << plotname << endl; 00058 continue; 00059 } 00060 00061 /// @todo Check that "path" matches filename 00062 vector<DPSXYPoint> points; 00063 for (const TiXmlNode* dpN = dpsN->FirstChild("dataPoint"); dpN; dpN = dpN->NextSibling()) { 00064 const TiXmlNode* xMeasN = dpN->FirstChild("measurement"); 00065 const TiXmlNode* yMeasN = xMeasN->NextSibling(); 00066 if (xMeasN && yMeasN) { 00067 const TiXmlElement* xMeasE = xMeasN->ToElement(); 00068 const TiXmlElement* yMeasE = yMeasN->ToElement(); 00069 const string xcentreStr = xMeasE->Attribute("value"); 00070 const string xerrplusStr = xMeasE->Attribute("errorPlus"); 00071 const string xerrminusStr = xMeasE->Attribute("errorMinus"); 00072 const string ycentreStr = yMeasE->Attribute("value"); 00073 const string yerrplusStr = yMeasE->Attribute("errorPlus"); 00074 const string yerrminusStr = yMeasE->Attribute("errorMinus"); 00075 //if (!centreStr) throw Error("Couldn't get a valid bin centre"); 00076 //if (!errplusStr) throw Error("Couldn't get a valid bin err+"); 00077 //if (!errminusStr) throw Error("Couldn't get a valid bin err-"); 00078 istringstream xssC(xcentreStr); 00079 istringstream xssP(xerrplusStr); 00080 istringstream xssM(xerrminusStr); 00081 istringstream yssC(ycentreStr); 00082 istringstream yssP(yerrplusStr); 00083 istringstream yssM(yerrminusStr); 00084 double xcentre, xerrplus, xerrminus, ycentre, yerrplus, yerrminus; 00085 xssC >> xcentre; xssP >> xerrplus; xssM >> xerrminus; 00086 yssC >> ycentre; yssP >> yerrplus; yssM >> yerrminus; 00087 //cout << " " << centre << " + " << errplus << " - " << errminus << endl; 00088 DPSXYPoint pt(xcentre, xerrminus, xerrplus, ycentre, yerrminus, yerrplus); 00089 points.push_back(pt); 00090 } else { 00091 cerr << "Couldn't get <measurement> tag" << endl; 00092 /// @todo Throw an exception here? 00093 } 00094 } 00095 00096 // Add to the map 00097 rtn[plotname] = points; 00098 } 00099 00100 } 00101 // Write out the error 00102 /// @todo Rethrow as a general XML failure. 00103 catch (std::exception& e) { 00104 cerr << e.what() << endl; 00105 throw; 00106 } 00107 00108 // Return 00109 return rtn; 00110 }
| HistoFormatList Rivet::getKnownHistoFormatEnums | ( | ) | [inline] |
Function which returns a vector of all the histogram format values in the HistoFormat enum.
Definition at line 49 of file HistoFormat.hh.
References getKnownHistoFormats().
00049 { 00050 HistoFormatList names; 00051 HistoFormatMap hfmap = getKnownHistoFormats(); 00052 for (HistoFormatMap::const_iterator hf = hfmap.begin(); hf != hfmap.end(); ++hf) { 00053 names.push_back(hf->first); 00054 } 00055 return names; 00056 }
| std::vector<std::string> Rivet::getKnownHistoFormatNames | ( | ) | [inline] |
Function which returns a vector of all the histogram format name strings.
Definition at line 60 of file HistoFormat.hh.
References getKnownHistoFormats().
00060 { 00061 vector<string> names; 00062 HistoFormatMap hfmap = getKnownHistoFormats(); 00063 for (HistoFormatMap::const_iterator hf = hfmap.begin(); hf != hfmap.end(); ++hf) { 00064 names.push_back(hf->second); 00065 } 00066 return names; 00067 }
| HistoFormatMap Rivet::getKnownHistoFormats | ( | ) | [inline] |
Function which returns a map from histogram format enums to the corresponding name strings.
Definition at line 22 of file HistoFormat.hh.
References AIDAML, FLAT, and ROOT.
Referenced by getKnownHistoFormatEnums(), getKnownHistoFormatNames(), and getKnownHistoFormatsR().
00022 { 00023 HistoFormatMap hfmap; 00024 hfmap[AIDAML] = "AIDA"; 00025 hfmap[FLAT] = "FLAT"; 00026 #ifdef HAVE_ROOT 00027 hfmap[ROOT] = "ROOT"; 00028 #endif 00029 return hfmap; 00030 }
| HistoFormatMapR Rivet::getKnownHistoFormatsR | ( | ) | [inline] |
Function which returns a map from histogram format name strings to the corresponding enums.
Definition at line 33 of file HistoFormat.hh.
References getKnownHistoFormats().
00033 { 00034 HistoFormatMap hfmap = getKnownHistoFormats(); 00035 HistoFormatMapR hfmapr; 00036 for (HistoFormatMap::const_iterator hf = hfmap.begin(); hf != hfmap.end(); ++hf) { 00037 hfmapr[hf->second] = hf->first; 00038 } 00039 return hfmapr; 00040 }
| string getLibPath | ( | ) |
Get library install path.
Definition at line 22 of file RivetPaths.cc.
| string getRivetDataPath | ( | ) |
Get Rivet data install path.
Definition at line 40 of file RivetPaths.cc.
Referenced by getAnalysisInfoPaths(), getAnalysisPlotPaths(), getAnalysisRefPaths(), and getDatafilePath().
| bool Rivet::hadronFilter | ( | const Particle & | p | ) |
Definition at line 16 of file HadronicFinalState.cc.
References Rivet::PID::isHadron(), and Particle::pdgId().
Referenced by HadronicFinalState::project().
00016 { 00017 return ! PID::isHadron(p.pdgId()); 00018 }
| int Rivet::index_between | ( | const NUM & | val, | |
| const vector< NUM > & | binedges | |||
| ) | [inline] |
Return the bin index of the given value, val, given a vector of bin edges NB. The binedges vector must be sorted.
Definition at line 236 of file MathUtils.hh.
References inRange().
Referenced by CDF_2008_S7782535::analyze(), and JetShape::calc().
00236 { 00237 if (!inRange(val, binedges.front(), binedges.back())) return -1; //< Out of histo range 00238 int index = -1; 00239 for (size_t i = 1; i < binedges.size(); ++i) { 00240 if (val < binedges[i]) { 00241 index = i-1; 00242 break; 00243 } 00244 } 00245 assert(inRange(index, -1, binedges.size()-1)); 00246 return index; 00247 }
| bool Rivet::inRange | ( | int | value, | |
| pair< int, int > | lowhigh, | |||
| RangeBoundary | lowbound = CLOSED, |
|||
| RangeBoundary | highbound = OPEN | |||
| ) | [inline] |
Alternative version of inRange for ints, which accepts a pair for the range arguments.
Definition at line 137 of file MathUtils.hh.
References inRange().
00138 { 00139 return inRange(value, lowhigh.first, lowhigh.second, lowbound, highbound); 00140 }
| bool Rivet::inRange | ( | int | value, | |
| int | low, | |||
| int | high, | |||
| RangeBoundary | lowbound = CLOSED, |
|||
| RangeBoundary | highbound = CLOSED | |||
| ) | [inline] |
Determine if value is in the range low to high, for integer types Interval boundary types are defined by lowbound and highbound.
- Todo:
- Optimise to one-line at compile time?
Definition at line 123 of file MathUtils.hh.
00124 { 00125 if (lowbound == OPEN && highbound == OPEN) { 00126 return (value > low && value < high); 00127 } else if (lowbound == OPEN && highbound == CLOSED) { 00128 return (value > low && value <= high); 00129 } else if (lowbound == CLOSED && highbound == OPEN) { 00130 return (value >= low && value < high); 00131 } else { // if (lowbound == CLOSED && highbound == CLOSED) { 00132 return (value >= low && value <= high); 00133 } 00134 }
| bool Rivet::inRange | ( | NUM | value, | |
| pair< NUM, NUM > | lowhigh, | |||
| RangeBoundary | lowbound = CLOSED, |
|||
| RangeBoundary | highbound = OPEN | |||
| ) | [inline] |
Alternative version of inRange for doubles, which accepts a pair for the range arguments.
Definition at line 114 of file MathUtils.hh.
References inRange().
00115 { 00116 return inRange(value, lowhigh.first, lowhigh.second, lowbound, highbound); 00117 }
| bool Rivet::inRange | ( | NUM | value, | |
| NUM | low, | |||
| NUM | high, | |||
| RangeBoundary | lowbound = CLOSED, |
|||
| RangeBoundary | highbound = OPEN | |||
| ) | [inline] |
Determine if value is in the range low to high, for floating point numbers Interval boundary types are defined by lowbound and highbound.
- Todo:
- Optimise to one-line at compile time?
Definition at line 99 of file MathUtils.hh.
References CLOSED, fuzzyEquals(), and OPEN.
Referenced by UA1_1990_S2044935::analyze(), STAR_2008_S7993412::analyze(), STAR_2006_S6870392::analyze(), MC_TTBAR::analyze(), H1_2000_S4129130::analyze(), D0_2008_S7719523::analyze(), D0_2004_S5992206::analyze(), D0_2001_S4674421::analyze(), CDF_2010_S8591881_DY::analyze(), CDF_2008_NOTE_9351::analyze(), CDF_2006_S6450792::analyze(), CDF_2004_S5839831::analyze(), JetShape::calc(), InvMassFinalState::calc(), JetShape::diffJetShape(), ATLAS_2011_S9120807::getEtaBin(), OPAL_2004_S6132243::getHistIndex(), index_between(), inRange(), JetShape::intJetShape(), JetAlg::jets(), linspace(), TriggerUA5::project(), TriggerCDFRun2::project(), TriggerCDFRun0Run1::project(), InitialQuarks::project(), JetShape::rBinMax(), JetShape::rBinMid(), JetShape::rBinMin(), ATLAS_2011_S8994773::region_index(), and ATLAS_2010_S8894728::region_index().
00100 { 00101 if (lowbound == OPEN && highbound == OPEN) { 00102 return (value > low && value < high); 00103 } else if (lowbound == OPEN && highbound == CLOSED) { 00104 return (value > low && (value < high || fuzzyEquals(value, high))); 00105 } else if (lowbound == CLOSED && highbound == OPEN) { 00106 return ((value > low || fuzzyEquals(value, low)) && value < high); 00107 } else { // if (lowbound == CLOSED && highbound == CLOSED) { 00108 return ((value > low || fuzzyEquals(value, low)) && (value < high || fuzzyEquals(value, high))); 00109 } 00110 }
| double Rivet::integral | ( | AIDA::IHistogram1D * | histo | ) | [inline] |
Return the integral over the histogram bins.
Definition at line 42 of file RivetAIDA.hh.
Referenced by JetShape::calc(), and D0_2001_S4674421::finalize().
| set<PdgIdPair> Rivet::intersection | ( | const set< PdgIdPair > & | a, | |
| const set< PdgIdPair > & | b | |||
| ) | [inline] |
Return the intersection of two sets of {PdgIdPair}s.
Definition at line 56 of file BeamConstraint.hh.
References compatible().
Referenced by Projection::beamPairs().
00056 { 00057 set<PdgIdPair> ret; 00058 for (set<PdgIdPair>::const_iterator bp = a.begin(); bp != a.end(); ++bp) { 00059 if (compatible(*bp, b)) ret.insert(*bp); 00060 } 00061 return ret; 00062 }
| Num Rivet::intpow | ( | Num | val, | |
| unsigned int | exp | |||
| ) | [inline] |
A more efficient version of pow for raising numbers to integer powers.
Definition at line 168 of file MathUtils.hh.
Referenced by ATLAS_2010_S8894728::analyze().
00168 { 00169 assert(exp >= 0); 00170 if (exp == 0) return (Num) 1; 00171 else if (exp == 1) return val; 00172 else return val * intpow(val, exp-1); 00173 }
| double Rivet::invariant | ( | const FourVector & | lv | ) | [inline] |
Calculate the Lorentz self-invariant of a 4-vector. 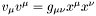 .
.
Definition at line 241 of file Vector4.hh.
References FourVector::invariant().
Referenced by DISKinematics::project().
| Matrix<N> Rivet::inverse | ( | const Matrix< N > & | m | ) | [inline] |
Definition at line 348 of file MatrixN.hh.
References Matrix< N >::inverse().
00348 { 00349 return m.inverse(); 00350 }
| LorentzTransform Rivet::inverse | ( | const LorentzTransform & | lt | ) | [inline] |
Definition at line 149 of file LorentzTrans.hh.
References LorentzTransform::inverse().
| bool Rivet::isZero | ( | const Vector< N > & | v, | |
| double | tolerance = 1E-5 | |||
| ) | [inline] |
External form of numerically safe nullness check.
Definition at line 201 of file VectorN.hh.
References Vector< N >::isZero().
| bool Rivet::isZero | ( | const Matrix< N > & | m, | |
| double | tolerance = 1E-5 | |||
| ) | [inline] |
External form of numerically safe nullness check.
Definition at line 411 of file MatrixN.hh.
References Matrix< N >::isZero().
00411 { 00412 return m.isZero(tolerance); 00413 }
| bool Rivet::isZero | ( | long | val, | |
| double | UNUSEDtolerance = 1E-8 | |||
| ) | [inline] |
Compare an integral-type number to zero. Since there is no risk of floating point error, this function just exists in case isZero is accidentally used on an integer type, to avoid implicit type conversion. The tolerance parameter is ignored.
Definition at line 25 of file MathUtils.hh.
| bool Rivet::isZero | ( | double | val, | |
| double | tolerance = 1E-8 | |||
| ) | [inline] |
Compare a floating point number to zero with a degree of fuzziness expressed by the absolute tolerance parameter.
Definition at line 17 of file MathUtils.hh.
Referenced by _mapAngleM2PITo2Pi(), CDF_2004_S5839831::analyze(), Vector3::angle(), Vector3::azimuthalAngle(), FinalState::FinalState(), Matrix< 4 >::isDiag(), Matrix< 4 >::isEqual(), Vector< 4 >::isZero(), Matrix< 4 >::isZero(), mapAngle0To2Pi(), mapAngle0ToPi(), mapAngleMPiToPi(), FourMomentum::mass(), UnstableFinalState::project(), DISKinematics::project(), rapidity(), Matrix3::setAsRotation(), sign(), and toString().
| vector<double> Rivet::linspace | ( | double | start, | |
| double | end, | |||
| size_t | nbins | |||
| ) | [inline] |
Make a list of nbins + 1 values equally spaced between start and end inclusive.
Definition at line 201 of file MathUtils.hh.
References CLOSED, and inRange().
Referenced by JetShape::JetShape(), and logspace().
00201 { 00202 assert(end >= start); 00203 assert(nbins > 0); 00204 vector<double> rtn; 00205 const double interval = (end-start)/static_cast<double>(nbins); 00206 double edge = start; 00207 while (inRange(edge, start, end, CLOSED, CLOSED)) { 00208 rtn.push_back(edge); 00209 edge += interval; 00210 } 00211 assert(rtn.size() == nbins+1); 00212 return rtn; 00213 }
| vector<double> Rivet::logspace | ( | double | start, | |
| double | end, | |||
| size_t | nbins | |||
| ) | [inline] |
Make a list of nbins + 1 values exponentially spaced between start and end inclusive.
Definition at line 217 of file MathUtils.hh.
References linspace().
00217 { 00218 assert(end >= start); 00219 assert(start > 0); 00220 assert(nbins > 0); 00221 const double logstart = std::log(start); 00222 const double logend = std::log(end); 00223 const vector<double> logvals = linspace(logstart, logend, nbins); 00224 vector<double> rtn; 00225 foreach (double logval, logvals) { 00226 rtn.push_back(std::exp(logval)); 00227 } 00228 assert(rtn.size() == nbins+1); 00229 return rtn; 00230 }
| double Rivet::lorentzGamma | ( | const double | beta | ) | [inline] |
Definition at line 15 of file LorentzTrans.hh.
Referenced by LorentzTransform::gamma(), and LorentzTransform::setBoost().
| std::pair<PdgId,PdgId> Rivet::make_pdgid_pair | ( | const std::string & | a, | |
| const std::string & | b | |||
| ) | [inline] |
Convenience maker of particle ID pairs from particle names.
Definition at line 159 of file ParticleName.hh.
References toParticleId().
00159 { 00160 const PdgId pa = toParticleId(a); 00161 const PdgId pb = toParticleId(b); 00162 return make_pair(pa, pb); 00163 }
Convenience maker of particle ID pairs from PdgIds.
Definition at line 153 of file ParticleName.hh.
Referenced by compatible(), and AnalysisInfo::make().
| double Rivet::mapAngle0To2Pi | ( | double | angle | ) | [inline] |
Map an angle into the range [0, 2PI).
Definition at line 363 of file MathUtils.hh.
References _mapAngleM2PITo2Pi(), isZero(), and TWOPI.
Referenced by CDF_2004_S5839831::_calcTransCones(), and D0_1996_S3324664::analyze().
| double Rivet::mapAngle0ToPi | ( | double | angle | ) | [inline] |
Map an angle into the range [0, PI].
Definition at line 373 of file MathUtils.hh.
References isZero(), mapAngleMPiToPi(), and PI.
Referenced by CDF_1997_S3541940::_psi(), CDF_1996_S3349578::_psi(), MC_ZZJETS::analyze(), MC_WWJETS::analyze(), MC_PHOTONJETS::analyze(), D0_2010_S8821313::analyze(), D0_2010_S8570965::analyze(), CDF_2005_S6080774::analyze(), ATLAS_2011_S9120807::analyze(), ATLAS_2011_S8971293::analyze(), and deltaPhi().
00373 { 00374 double rtn = fabs(mapAngleMPiToPi(angle)); 00375 if (isZero(rtn)) return 0; 00376 assert(rtn > 0 && rtn <= PI); 00377 return rtn; 00378 }
| double Rivet::mapAngleMPiToPi | ( | double | angle | ) | [inline] |
Map an angle into the range (-PI, PI].
Definition at line 353 of file MathUtils.hh.
References _mapAngleM2PITo2Pi(), isZero(), PI, and TWOPI.
Referenced by Jet::_calcPtAvgs(), MC_SUSY::analyze(), and mapAngle0ToPi().
| double Rivet::mass | ( | const FourMomentum & | v | ) | [inline] |
Get the mass 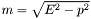 (the Lorentz self-invariant) of a momentum 4-vector.
(the Lorentz self-invariant) of a momentum 4-vector.
Definition at line 540 of file Vector4.hh.
References FourMomentum::mass().
Referenced by MC_WWJETS::analyze(), MC_TTBAR::analyze(), D0_2001_S4674421::analyze(), CDF_2010_S8591881_DY::analyze(), CDF_2008_NOTE_9351::analyze(), CDF_1996_S3108457::analyze(), ATLAS_2010_S8817804::analyze(), mt2::mt2_massless(), and VetoedFinalState::project().
| double Rivet::mass2 | ( | const FourMomentum & | v | ) | [inline] |
Get the squared mass  (the Lorentz self-invariant) of a momentum 4-vector.
(the Lorentz self-invariant) of a momentum 4-vector.
Definition at line 550 of file Vector4.hh.
References FourMomentum::mass2().
Referenced by CDF_1997_S3541940::_reduce(), CDF_1996_S3349578::_reduce(), D0_1996_S3214044::_safeMass(), CDF_1997_S3541940::_safeMass(), CDF_1996_S3349578::_safeMass(), and VetoedFinalState::project().
| double Rivet::massT | ( | const FourMomentum & | v | ) | [inline] |
Get the transverse mass 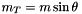 of a momentum 4-vector.
of a momentum 4-vector.
Definition at line 545 of file Vector4.hh.
References FourMomentum::massT().
| double Rivet::massT2 | ( | const FourMomentum & | v | ) | [inline] |
Get the squared transverse mass 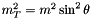 of a momentum 4-vector.
of a momentum 4-vector.
Definition at line 555 of file Vector4.hh.
References FourMomentum::massT2().
| double Rivet::mean | ( | const vector< int > & | sample | ) | [inline] |
Calculate the mean of a sample.
Definition at line 256 of file MathUtils.hh.
Referenced by covariance(), and covariance_err().
00256 { 00257 double mean = 0.0; 00258 for (size_t i=0; i<sample.size(); ++i) { 00259 mean += sample[i]; 00260 } 00261 return mean/sample.size(); 00262 }
| double Rivet::mean_err | ( | const vector< int > & | sample | ) | [inline] |
Definition at line 265 of file MathUtils.hh.
Referenced by covariance_err().
| double Rivet::mod | ( | const Vector< N > & | v | ) | [inline] |
Calculate the modulus of a vector. 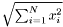 .
.
Definition at line 150 of file VectorN.hh.
References Vector< N >::mod().
Referenced by FParameter::_calcFParameter(), Spherocity::_calcSpherocity(), _calcT(), Thrust::_calcThrust(), D0_1996_S3214044::_fourJetAnalysis(), Hemispheres::project(), and unit().
| double Rivet::mod2 | ( | const Vector< N > & | v | ) | [inline] |
Calculate the modulus-squared of a vector. 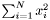 .
.
Definition at line 143 of file VectorN.hh.
References Vector< N >::mod2().
| bool Rivet::mod2Cmp | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Definition at line 42 of file Thrust.cc.
References Vector< N >::mod2().
| bool Rivet::mod2Cmp | ( | const Vector< 2 > & | a, | |
| const Vector< 2 > & | b | |||
| ) | [inline] |
Definition at line 45 of file Spherocity.cc.
References Vector< N >::mod2().
Referenced by _calcT().
| FourMomentum Rivet::momentum | ( | const fastjet::PseudoJet & | pj | ) | [inline] |
Make a 4-momentum vector from a FastJet pseudo-jet.
Definition at line 36 of file FastJets.hh.
Referenced by D0_1996_S3214044::_fourJetAnalysis(), D0_1996_S3214044::_threeJetAnalysis(), STAR_2009_UE_HELEN::analyze(), OPAL_1993_S2692198::analyze(), MC_ZZJETS::analyze(), MC_ZJETS::analyze(), MC_WWJETS::analyze(), MC_WJETS::analyze(), MC_TTBAR::analyze(), MC_PHOTONJETS::analyze(), MC_LEADINGJETS::analyze(), MC_JetAnalysis::analyze(), MC_HJETS::analyze(), MC_DIPHOTON::analyze(), MC_DIJET::analyze(), D0_2010_S8566488::analyze(), D0_2009_S8320160::analyze(), D0_2009_S8202443::analyze(), D0_2008_S7863608::analyze(), D0_2007_S7075677::analyze(), D0_2004_S5992206::analyze(), D0_1996_S3214044::analyze(), CMS_2011_S8968497::analyze(), CMS_2011_S8957746::analyze(), CDF_2010_S8591881_QCD::analyze(), CDF_2010_S8591881_DY::analyze(), CDF_2008_S8095620::analyze(), CDF_2008_S8093652::analyze(), CDF_2008_S7540469::analyze(), CDF_2008_NOTE_9351::analyze(), CDF_2008_LEADINGJETS::analyze(), CDF_2006_S6653332::analyze(), CDF_2005_S6080774::analyze(), CDF_2004_S5839831::analyze(), CDF_1994_S2952106::analyze(), ATLAS_2011_S8971293::analyze(), ATLAS_2011_CONF_2011_090::analyze(), and ATLAS_2010_S8919674::analyze().
| Vector3 Rivet::momentum3 | ( | const fastjet::PseudoJet & | pj | ) | [inline] |
Make a 3-momentum vector from a FastJet pseudo-jet.
Definition at line 31 of file FastJets.hh.
| FourMomentum Rivet::multiply | ( | const FourMomentum & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 507 of file Vector4.hh.
References multiply().
00507 { 00508 return multiply(a, v); 00509 }
| FourMomentum Rivet::multiply | ( | const double | a, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Definition at line 501 of file Vector4.hh.
References Vector< N >::_vec.
| FourVector Rivet::multiply | ( | const FourVector & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 209 of file Vector4.hh.
References multiply().
00209 { 00210 return multiply(a, v); 00211 }
| FourVector Rivet::multiply | ( | const double | a, | |
| const FourVector & | v | |||
| ) | [inline] |
Definition at line 203 of file Vector4.hh.
References Vector< N >::_vec.
| Vector3 multiply | ( | const Vector3 & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 230 of file Vector3.hh.
References multiply().
00230 { 00231 return multiply(a, v); 00232 }
| Vector3 multiply | ( | const double | a, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 224 of file Vector3.hh.
References Vector< N >::_vec.
| Vector< N > multiply | ( | const Matrix< N > & | a, | |
| const Vector< N > & | b | |||
| ) | [inline] |
| Matrix<N> Rivet::multiply | ( | const Matrix< N > & | m, | |
| const double | a | |||
| ) | [inline] |
Definition at line 291 of file MatrixN.hh.
References multiply().
| Matrix<N> Rivet::multiply | ( | const double | a, | |
| const Matrix< N > & | m | |||
| ) | [inline] |
Definition at line 284 of file MatrixN.hh.
References Matrix< N >::_matrix.
00284 { 00285 Matrix<N> rtn; 00286 rtn._matrix = a * m._matrix; 00287 return rtn; 00288 }
| Matrix< N > multiply | ( | const Matrix< N > & | a, | |
| const Matrix< N > & | b | |||
| ) | [inline] |
Definition at line 311 of file MatrixN.hh.
References Matrix< N >::_matrix.
Referenced by divide(), multiply(), operator*(), operator/(), LorentzTransform::preMult(), and LorentzTransform::transform().
| int Rivet::nocase_cmp | ( | const string & | s1, | |
| const string & | s2 | |||
| ) | [inline] |
Definition at line 14 of file Utils.hh.
00014 { 00015 string::const_iterator it1 = s1.begin(); 00016 string::const_iterator it2 = s2.begin(); 00017 while ( (it1 != s1.end()) && (it2 != s2.end()) ) { 00018 if(::toupper(*it1) != ::toupper(*it2)) { // < Letters differ? 00019 // Return -1 to indicate smaller than, 1 otherwise 00020 return (::toupper(*it1) < ::toupper(*it2)) ? -1 : 1; 00021 } 00022 // Proceed to the next character in each string 00023 ++it1; 00024 ++it2; 00025 } 00026 size_t size1 = s1.size(), size2 = s2.size(); // Cache lengths 00027 // Return -1,0 or 1 according to strings' lengths 00028 if (size1 == size2) return 0; 00029 return (size1 < size2) ? -1 : 1; 00030 }
| FourMomentum Rivet::operator* | ( | const FourMomentum & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 515 of file Vector4.hh.
References multiply().
00515 { 00516 return multiply(a, v); 00517 }
| FourMomentum Rivet::operator* | ( | const double | a, | |
| const FourMomentum & | v | |||
| ) | [inline] |
Definition at line 511 of file Vector4.hh.
References multiply().
00511 { 00512 return multiply(a, v); 00513 }
| FourVector Rivet::operator* | ( | const FourVector & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 217 of file Vector4.hh.
References multiply().
00217 { 00218 return multiply(a, v); 00219 }
| FourVector Rivet::operator* | ( | const double | a, | |
| const FourVector & | v | |||
| ) | [inline] |
Definition at line 213 of file Vector4.hh.
References multiply().
00213 { 00214 return multiply(a, v); 00215 }
| Vector3 operator* | ( | const Vector3 & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 238 of file Vector3.hh.
References multiply().
00238 { 00239 return multiply(a, v); 00240 }
| Vector3 operator* | ( | const double | a, | |
| const Vector3 & | v | |||
| ) | [inline] |
Definition at line 234 of file Vector3.hh.
References multiply().
00234 { 00235 return multiply(a, v); 00236 }
| Vector<N> Rivet::operator* | ( | const Matrix< N > & | a, | |
| const Vector< N > & | b | |||
| ) | [inline] |
Definition at line 331 of file MatrixN.hh.
References multiply().
00331 { 00332 return multiply(a, b); 00333 }
| Matrix<N> Rivet::operator* | ( | const Matrix< N > & | m, | |
| const double | a | |||
| ) | [inline] |
Definition at line 306 of file MatrixN.hh.
References multiply().
| Matrix<N> Rivet::operator* | ( | const double | a, | |
| const Matrix< N > & | m | |||
| ) | [inline] |
Definition at line 301 of file MatrixN.hh.
References multiply().
| Matrix< N > operator* | ( | const Matrix< N > & | a, | |
| const Matrix< N > & | b | |||
| ) | [inline] |
Definition at line 318 of file MatrixN.hh.
References multiply().
00318 { 00319 return multiply(a, b); 00320 }
| FourMomentum Rivet::operator+ | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 529 of file Vector4.hh.
References add().
00529 { 00530 return add(a, b); 00531 }
| FourVector Rivet::operator+ | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Definition at line 231 of file Vector4.hh.
References add().
00231 { 00232 return add(a, b); 00233 }
| Vector3 operator+ | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Definition at line 258 of file Vector3.hh.
References add().
00258 { 00259 return add(a, b); 00260 }
| Matrix<N> Rivet::operator+ | ( | const Matrix< N > | a, | |
| const Matrix< N > & | b | |||
| ) | [inline] |
Definition at line 274 of file MatrixN.hh.
References add().
00274 { 00275 return add(a, b); 00276 }
| FourMomentum Rivet::operator- | ( | const FourMomentum & | a, | |
| const FourMomentum & | b | |||
| ) | [inline] |
Definition at line 533 of file Vector4.hh.
References add().
00533 { 00534 return add(a, -b); 00535 }
| FourVector Rivet::operator- | ( | const FourVector & | a, | |
| const FourVector & | b | |||
| ) | [inline] |
Definition at line 235 of file Vector4.hh.
References add().
00235 { 00236 return add(a, -b); 00237 }
| Vector3 operator- | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Definition at line 262 of file Vector3.hh.
References subtract().
00262 { 00263 return subtract(a, b); 00264 }
| Matrix<N> Rivet::operator- | ( | const Matrix< N > | a, | |
| const Matrix< N > & | b | |||
| ) | [inline] |
Definition at line 279 of file MatrixN.hh.
References subtract().
00279 { 00280 return subtract(a, b); 00281 }
| FourMomentum Rivet::operator/ | ( | const FourMomentum & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 519 of file Vector4.hh.
References multiply().
00519 { 00520 return multiply(1.0/a, v); 00521 }
| FourVector Rivet::operator/ | ( | const FourVector & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 221 of file Vector4.hh.
References multiply().
00221 { 00222 return multiply(1.0/a, v); 00223 }
| Vector3 operator/ | ( | const Vector3 & | v, | |
| const double | a | |||
| ) | [inline] |
Definition at line 242 of file Vector3.hh.
References multiply().
00242 { 00243 return multiply(1.0/a, v); 00244 }
| ostream & operator<< | ( | Log & | log, | |
| int | level | |||
| ) |
Streaming output to a logger must have a Log::Level/int as its first argument.
The streaming operator can use Log's internals.
Definition at line 189 of file Logging.cc.
References Log::_nostream, Log::formatMessage(), and Log::isActive().
| std::ostream& Rivet::operator<< | ( | std::ostream & | os, | |
| const std::list< T > & | vec | |||
| ) | [inline] |
| std::ostream& Rivet::operator<< | ( | std::ostream & | os, | |
| const std::vector< T > & | vec | |||
| ) | [inline] |
| std::ostream& Rivet::operator<< | ( | std::ostream & | os, | |
| const ParticlePair & | pp | |||
| ) | [inline] |
Allow ParticlePair to be passed to an ostream.
Definition at line 125 of file Particle.hh.
References toString().
00125 { 00126 os << toString(pp); 00127 return os; 00128 }
| std::ostream& Rivet::operator<< | ( | std::ostream & | out, | |
| const Vector< N > & | v | |||
| ) | [inline] |
Stream out string representation.
Definition at line 176 of file VectorN.hh.
References toString().
00176 { 00177 out << toString(v); 00178 return out; 00179 }
| std::ostream& Rivet::operator<< | ( | std::ostream & | out, | |
| const FourVector & | lv | |||
| ) | [inline] |
Write a 4-vector to an ostream.
Definition at line 937 of file Vector4.hh.
References toString().
00937 { 00938 out << toString(lv); 00939 return out; 00940 }
| ostream& Rivet::operator<< | ( | std::ostream & | out, | |
| const Matrix< N > & | m | |||
| ) | [inline] |
Stream out string representation.
Definition at line 386 of file MatrixN.hh.
References m, and toString().
| ostream& Rivet::operator<< | ( | std::ostream & | out, | |
| const typename EigenSystem< N >::EigenPair & | e | |||
| ) | [inline] |
Definition at line 166 of file MatrixDiag.hh.
References toString().
00166 { 00167 out << toString(e); 00168 return out; 00169 }
| ostream& Rivet::operator<< | ( | std::ostream & | out, | |
| const LorentzTransform & | lt | |||
| ) | [inline] |
Definition at line 169 of file LorentzTrans.hh.
References toString().
00169 { 00170 out << toString(lt); 00171 return out; 00172 }
| std::ostream& Rivet::operator<< | ( | std::ostream & | os, | |
| const AnalysisInfo & | ai | |||
| ) | [inline] |
Stream an AnalysisInfo as a text description.
Definition at line 233 of file AnalysisInfo.hh.
References toString().
00233 { 00234 os << toString(ai); 00235 return os; 00236 }
| vector<GenParticle*> Rivet::particles | ( | GenVertex * | gv, | |
| HepMC::IteratorRange | range = HepMC::relatives | |||
| ) | [inline] |
| vector<GenParticle*> Rivet::particles | ( | const GenEvent * | ge | ) | [inline] |
Definition at line 26 of file RivetHepMC.hh.
References particles().
00026 { 00027 assert(ge); 00028 return particles(*ge); 00029 }
| vector<GenParticle*> Rivet::particles | ( | const GenEvent & | ge | ) | [inline] |
Definition at line 19 of file RivetHepMC.hh.
References pi.
Referenced by OPAL_2001_S4553896::analyze(), MC_PHOTONJETS::analyze(), MC_GENERIC::analyze(), MC_DIPHOTON::analyze(), JADE_OPAL_2000_S4300807::analyze(), H1_2000_S4129130::analyze(), H1_1994_S2919893::analyze(), DELPHI_2002_069_CONF_603::analyze(), D0_2010_S8570965::analyze(), D0_2008_S7719523::analyze(), D0_2006_S6438750::analyze(), CDF_2009_S8436959::analyze(), CDF_2008_S8095620::analyze(), CDF_2005_S6080774::analyze(), CDF_2004_S5839831::analyze(), CDF_1993_S2742446::analyze(), ATLAS_2011_S9120807::analyze(), ATLAS_2011_S9019561::analyze(), ATLAS_2011_S8983313::analyze(), ATLAS_2011_CONF_2011_090::analyze(), ATLAS_2010_S8919674::analyze(), ATLAS_2010_S8914702::analyze(), ALEPH_1996_S3196992::analyze(), Jet::containsBottom(), Jet::containsCharm(), Particle::hasAncestor(), particles(), UnstableFinalState::project(), Thrust::project(), Spherocity::project(), Sphericity::project(), InitialQuarks::project(), Hemispheres::project(), FParameter::project(), FinalState::project(), FastJets::project(), and BeamThrust::project().
| const std::pair<GenVertex::particles_in_const_iterator, GenVertex::particles_in_const_iterator> Rivet::particles_in | ( | const GenVertex * | gv | ) | [inline] |
Definition at line 59 of file RivetHepMC.hh.
Referenced by InitialQuarks::project().
| const std::pair<GenVertex::particles_out_const_iterator, GenVertex::particles_out_const_iterator> Rivet::particles_out | ( | const GenVertex * | gv | ) | [inline] |
Definition at line 64 of file RivetHepMC.hh.
Referenced by InitialQuarks::project().
| string Rivet::pathjoin | ( | const vector< string > & | paths | ) | [inline] |
Join several filesystem paths together with a delimiter character. Note that this does NOT join path elements together with a platform-portable directory delimiter, cf. the Python {os.path.join}!
Definition at line 85 of file Utils.hh.
Referenced by setAnalysisLibPaths().
| vector<string> Rivet::pathsplit | ( | const string & | path | ) | [inline] |
Split a path string with colon delimiters. Ignores zero-length substrings. Designed for getting elements of filesystem paths, naturally.
Definition at line 62 of file Utils.hh.
Referenced by getAnalysisInfoPaths(), getAnalysisPlotPaths(), getAnalysisRefPaths(), and split().
00062 { 00063 const string delim = ":"; 00064 vector<string> dirs; 00065 string tmppath = path; 00066 while (true) { 00067 const size_t delim_pos = tmppath.find(delim); 00068 if (delim_pos == string::npos) break; 00069 const string dir = tmppath.substr(0, delim_pos); 00070 if (dir.length()) dirs.push_back(dir); // Don't insert "empties" 00071 tmppath.replace(0, delim_pos+1, ""); 00072 } 00073 if (tmppath.length()) dirs.push_back(tmppath); // Don't forget the trailing component! 00074 return dirs; 00075 }
| const PROJ* Rivet::pcast | ( | const Projection * | p | ) | [inline] |
Convenience method for casting to a const Projection pointer.
Definition at line 38 of file Projection.fhh.
| const PROJ& Rivet::pcast | ( | const Projection & | p | ) | [inline] |
Convenience method for casting to a const Projection reference.
Definition at line 31 of file Projection.fhh.
| Cmp<Projection> Rivet::pcmp | ( | const Projection * | parent1, | |
| const Projection * | parent2, | |||
| const string & | pname | |||
| ) | [inline] |
Global helper function for easy creation of Cmp<Projection> objects from two parent projections and their common name for the projection to be compared.
Definition at line 320 of file Cmp.hh.
References ProjectionApplier::getProjection().
| Cmp<Projection> Rivet::pcmp | ( | const Projection & | parent1, | |
| const Projection * | parent2, | |||
| const string & | pname | |||
| ) | [inline] |
Global helper function for easy creation of Cmp<Projection> objects from two parent projections and their common name for the projection to be compared. This version takes one parent as a pointer.
Definition at line 313 of file Cmp.hh.
References ProjectionApplier::getProjection().
| Cmp<Projection> Rivet::pcmp | ( | const Projection * | parent1, | |
| const Projection & | parent2, | |||
| const string & | pname | |||
| ) | [inline] |
Global helper function for easy creation of Cmp<Projection> objects from two parent projections and their common name for the projection to be compared. This version takes one parent as a pointer.
Definition at line 305 of file Cmp.hh.
References ProjectionApplier::getProjection().
| Cmp<Projection> Rivet::pcmp | ( | const Projection & | parent1, | |
| const Projection & | parent2, | |||
| const string & | pname | |||
| ) | [inline] |
Global helper function for easy creation of Cmp<Projection> objects from two parent projections and their common name for the projection to be compared.
Definition at line 298 of file Cmp.hh.
References ProjectionApplier::getProjection().
| Cmp<Projection> Rivet::pcmp | ( | const Projection & | p1, | |
| const Projection & | p2 | |||
| ) | [inline] |
Global helper function for easy creation of Cmp<Projection> objects.
Definition at line 292 of file Cmp.hh.
Referenced by ProjectionHandler::_getEquiv(), Projection::mkNamedPCmp(), and Projection::mkPCmp().
| double Rivet::perp | ( | const FourVector & | v | ) | [inline] |
| double Rivet::perp | ( | const Vector3 & | v | ) | [inline] |
| double Rivet::perp2 | ( | const FourVector & | v | ) | [inline] |
Synonym for polarRadius2.
Definition at line 265 of file Vector4.hh.
References FourVector::perp2().
| double Rivet::perp2 | ( | const Vector3 & | v | ) | [inline] |
| double Rivet::phi | ( | const FourVector & | v, | |
| const PhiMapping | mapping = ZERO_2PI | |||
| ) | [inline] |
Synonym for azimuthalAngle.
Definition at line 291 of file Vector4.hh.
References FourVector::phi().
| double Rivet::phi | ( | const Vector3 & | v, | |
| const PhiMapping | mapping = ZERO_2PI | |||
| ) | [inline] |
Synonym for azimuthalAngle.
Definition at line 306 of file Vector3.hh.
References Vector3::phi().
Referenced by STAR_2009_UE_HELEN::analyze(), MC_LEADINGJETS::analyze(), MC_DIPHOTON::analyze(), D0_2004_S5992206::analyze(), CDF_2010_S8591881_QCD::analyze(), CDF_2008_LEADINGJETS::analyze(), CDF_2005_S6080774::analyze(), CDF_1994_S2952106::analyze(), ATLAS_2011_S8971293::analyze(), and ATLAS_2011_CONF_2011_090::analyze().
| double Rivet::polarAngle | ( | const FourVector & | v | ) | [inline] |
Calculate polar angle of a Lorentz vector.
Definition at line 297 of file Vector4.hh.
References FourVector::polarAngle().
| double Rivet::polarAngle | ( | const Vector3 & | v | ) | [inline] |
Calculate polar angle of a 3-vector.
Definition at line 311 of file Vector3.hh.
References Vector3::polarAngle().
| double Rivet::polarRadius | ( | const FourVector & | v | ) | [inline] |
Calculate transverse length 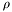 of a Lorentz vector.
of a Lorentz vector.
Definition at line 274 of file Vector4.hh.
References FourVector::polarRadius().
| double Rivet::polarRadius | ( | const Vector3 & | v | ) | [inline] |
Calculate transverse length 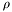 of a 3-vector.
of a 3-vector.
Definition at line 287 of file Vector3.hh.
References Vector3::polarRadius().
| double Rivet::polarRadius2 | ( | const FourVector & | v | ) | [inline] |
Calculate transverse length sq. 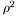 of a Lorentz vector.
of a Lorentz vector.
Definition at line 261 of file Vector4.hh.
References FourVector::polarRadius2().
| double Rivet::polarRadius2 | ( | const Vector3 & | v | ) | [inline] |
Calculate transverse length sq. 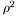 of a 3-vector.
of a 3-vector.
Definition at line 274 of file Vector3.hh.
References Vector3::polarRadius2().
| double Rivet::pseudorapidity | ( | const FourVector & | v | ) | [inline] |
Calculate pseudorapidity of a Lorentz vector.
Definition at line 306 of file Vector4.hh.
References FourVector::pseudorapidity().
| double Rivet::pseudorapidity | ( | const Vector3 & | v | ) | [inline] |
Calculate pseudorapidity of a 3-vector.
Definition at line 320 of file Vector3.hh.
References Vector3::pseudorapidity().
Referenced by MC_LEADINGJETS::analyze(), MC_DIJET::analyze(), CDF_2008_S7540469::analyze(), and CDF_2004_S5839831::analyze().
| double Rivet::pT | ( | const FourMomentum & | v | ) | [inline] |
Calculate the transverse momentum 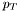 of a momentum 4-vector.
of a momentum 4-vector.
Definition at line 570 of file Vector4.hh.
References FourMomentum::pT().
Referenced by FinalState::accept(), STAR_2009_UE_HELEN::analyze(), STAR_2008_S7869363::analyze(), STAR_2006_S6860818::analyze(), STAR_2006_S6500200::analyze(), MC_TTBAR::analyze(), MC_PHOTONJETUE::analyze(), MC_LEADINGJETS::analyze(), MC_JetAnalysis::analyze(), MC_DIPHOTON::analyze(), MC_DIJET::analyze(), LHCB_2010_S8758301::analyze(), H1_1994_S2919893::analyze(), DELPHI_1996_S3430090::analyze(), D0_2009_S8202443::analyze(), D0_2008_S7863608::analyze(), D0_2008_S6879055::analyze(), CMS_2011_S8978280::analyze(), CMS_2011_S8957746::analyze(), CMS_2011_S8884919::analyze(), CMS_2010_S8656010::analyze(), CMS_2010_S8547297::analyze(), CDF_2010_S8591881_QCD::analyze(), CDF_2010_S8591881_DY::analyze(), CDF_2009_S8233977::analyze(), CDF_2008_NOTE_9351::analyze(), CDF_2008_LEADINGJETS::analyze(), CDF_2002_S4796047::analyze(), CDF_2001_S4751469::analyze(), ATLAS_2011_S8994773::analyze(), ATLAS_2011_S8971293::analyze(), ATLAS_2011_CONF_2011_090::analyze(), ATLAS_2010_S8919674::analyze(), ATLAS_2010_S8894728::analyze(), ATLAS_2010_S8817804::analyze(), ATLAS_2010_S8591806::analyze(), ALICE_2010_S8706239::analyze(), and InitialQuarks::project().
| double Rivet::pT2 | ( | const FourMomentum & | v | ) | [inline] |
Calculate the squared transverse momentum 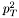 of a momentum 4-vector.
of a momentum 4-vector.
Definition at line 565 of file Vector4.hh.
References FourMomentum::pT2().
Referenced by H1_1994_S2919893::analyze().
| double Rivet::rapidity | ( | const FourMomentum & | v | ) | [inline] |
Calculate the rapidity of a momentum 4-vector.
Definition at line 560 of file Vector4.hh.
References FourMomentum::rapidity().
| double Rivet::rapidity | ( | double | E, | |
| double | pz | |||
| ) | [inline] |
Calculate a rapidity value from the supplied energy E and longitudinal momentum pz.
Definition at line 406 of file MathUtils.hh.
References isZero(), and MAXDOUBLE.
Referenced by MC_GENERIC::analyze(), D0_2008_S7863608::analyze(), CDF_2008_S8095620::analyze(), CDF_2006_S6653332::analyze(), ATLAS_2011_S8971293::analyze(), and deltaR().
| double Rivet::rho | ( | const FourVector & | v | ) | [inline] |
| double Rivet::rho | ( | const Vector3 & | v | ) | [inline] |
| double Rivet::rho2 | ( | const FourVector & | v | ) | [inline] |
| double Rivet::rho2 | ( | const Vector3 & | v | ) | [inline] |
| void setAnalysisLibPaths | ( | const std::vector< std::string > & | paths | ) |
Set the Rivet analysis plugin library search paths.
Definition at line 46 of file RivetPaths.cc.
References pathjoin().
00048 { 00049 const string pathstr = pathjoin(paths);
| int Rivet::sign | ( | long | val | ) | [inline] |
| int Rivet::sign | ( | int | val | ) | [inline] |
| int Rivet::sign | ( | double | val | ) | [inline] |
Find the sign of a number.
Definition at line 176 of file MathUtils.hh.
References isZero(), MINUS, PLUS, and ZERO.
Referenced by _calcT(), MC_PHOTONJETUE::analyze(), D0_2008_S7719523::analyze(), and CDF_1994_S2952106::analyze().
| vector<string> Rivet::split | ( | const string & | path, | |
| const string & | UNUSEDdelim = ":" | |||
| ) | [inline] |
- Deprecated:
- Use
pathsplitinstead.
Definition at line 78 of file Utils.hh.
References pathsplit().
Referenced by FastJets::splitJet().
| NUM Rivet::sqr | ( | NUM | a | ) | [inline] |
Named number-type squaring operation.
Definition at line 150 of file MathUtils.hh.
Referenced by OPAL_1993_S2692198::analyze(), MC_WPOL::analyze(), H1_1994_S2919893::analyze(), D0_2010_S8821313::analyze(), CDF_1994_S2952106::analyze(), BELLE_2006_S6265367::analyze(), deltaR(), get2dClosestApproach(), get2dDecayLength(), get3dClosestApproach(), get3dDecayLength(), and sqrtS().
| double sqrtS | ( | const FourMomentum & | pa, | |
| const FourMomentum & | pb | |||
| ) |
Function to get beam centre of mass energy from a pair of beam momenta.
Definition at line 35 of file Beam.cc.
References FourMomentum::E(), FourMomentum::pz(), and sqr().
| double sqrtS | ( | const ParticlePair & | beams | ) |
| double sqrtS | ( | const Event & | e | ) |
Function to get beam centre of mass energy from an event.
Definition at line 25 of file Beam.cc.
References Beam::project(), and Beam::sqrtS().
Referenced by sqrtS().
| bool Rivet::startsWith | ( | const string & | s, | |
| const string & | start | |||
| ) | [inline] |
| Vector3 Rivet::subtract | ( | const Vector3 & | a, | |
| const Vector3 & | b | |||
| ) | [inline] |
Definition at line 252 of file Vector3.hh.
References Vector< N >::_vec.
| Matrix<N> Rivet::subtract | ( | const Matrix< N > & | a, | |
| const Matrix< N > & | b | |||
| ) | [inline] |
Definition at line 269 of file MatrixN.hh.
References add().
Referenced by operator-().
00269 { 00270 return add(a, -b); 00271 }
| double Rivet::theta | ( | const FourVector & | v | ) | [inline] |
| double Rivet::theta | ( | const Vector3 & | v | ) | [inline] |
Synonym for polarAngle.
Definition at line 315 of file Vector3.hh.
References Vector3::theta().
Referenced by JADE_1998_S3612880::analyze(), mt2::mt2_massless(), and Matrix3::setAsRotation().
| std::string Rivet::toBeamsString | ( | const PdgIdPair & | pair | ) | [inline] |
Print a PdgIdPair as a string.
Definition at line 167 of file ParticleName.hh.
References toParticleName().
Referenced by AnalysisHandler::analyze().
00167 { 00168 string out = "[" + 00169 toParticleName(pair.first) + ", " + 00170 toParticleName(pair.second) + "]"; 00171 return out; 00172 }
| string Rivet::toLower | ( | const string & | s | ) | [inline] |
Definition at line 33 of file Utils.hh.
References transform().
| PdgId Rivet::toParticleId | ( | const std::string & | pname | ) | [inline] |
Print a PdgId as a named string.
Definition at line 147 of file ParticleName.hh.
References ParticleNames::particleId().
Referenced by make_pdgid_pair().
| const std::string& Rivet::toParticleName | ( | PdgId | p | ) | [inline] |
Print a PdgId as a named string.
Definition at line 141 of file ParticleName.hh.
References ParticleNames::particleName().
Referenced by toBeamsString(), and toString().
| std::string Rivet::toString | ( | const ParticlePair & | pair | ) | [inline] |
Print a ParticlePair as a string.
Definition at line 114 of file Particle.hh.
References GeV, and toParticleName().
00114 { 00115 stringstream out; 00116 out << "[" 00117 << toParticleName(pair.first.pdgId()) << " @ " 00118 << pair.first.momentum().E()/GeV << " GeV, " 00119 << toParticleName(pair.second.pdgId()) << " @ " 00120 << pair.second.momentum().E()/GeV << " GeV]"; 00121 return out.str(); 00122 }
| const string Rivet::toString | ( | const Vector< N > & | v | ) | [inline] |
Make string representation.
Definition at line 163 of file VectorN.hh.
References Vector< N >::size().
| const string Rivet::toString | ( | const FourVector & | lv | ) | [inline] |
Render a 4-vector as a string.
Definition at line 926 of file Vector4.hh.
References FourVector::t(), FourVector::x(), FourVector::y(), and FourVector::z().
00926 { 00927 ostringstream out; 00928 out << "(" << (fabs(lv.t()) < 1E-30 ? 0.0 : lv.t()) 00929 << "; " << (fabs(lv.x()) < 1E-30 ? 0.0 : lv.x()) 00930 << ", " << (fabs(lv.y()) < 1E-30 ? 0.0 : lv.y()) 00931 << ", " << (fabs(lv.z()) < 1E-30 ? 0.0 : lv.z()) 00932 << ")"; 00933 return out.str(); 00934 }
| string Rivet::toString | ( | const Matrix< N > & | m | ) | [inline] |
Make string representation.
Definition at line 368 of file MatrixN.hh.
References Matrix< N >::get(), isZero(), and Matrix< N >::size().
00368 { 00369 ostringstream ss; 00370 ss << "[ "; 00371 for (size_t i = 0; i < m.size(); ++i) { 00372 ss << "( "; 00373 for (size_t j = 0; j < m.size(); ++j) { 00374 const double e = m.get(i, j); 00375 ss << (Rivet::isZero(e) ? 0.0 : e) << " "; 00376 } 00377 ss << ") "; 00378 } 00379 ss << "]"; 00380 return ss.str(); 00381 }
| const string Rivet::toString | ( | const typename EigenSystem< N >::EigenPair & | e | ) | [inline] |
Definition at line 156 of file MatrixDiag.hh.
| string Rivet::toString | ( | const LorentzTransform & | lt | ) | [inline] |
Definition at line 165 of file LorentzTrans.hh.
References LorentzTransform::_boostMatrix, and toString().
00165 { 00166 return toString(lt._boostMatrix); 00167 }
| string toString | ( | const AnalysisInfo & | ai | ) |
String representation.
Definition at line 171 of file AnalysisInfo.cc.
References AnalysisInfo::name(), AnalysisInfo::status(), and AnalysisInfo::summary().
Referenced by operator<<(), and toString().
| string Rivet::toUpper | ( | const string & | s | ) | [inline] |
Definition at line 40 of file Utils.hh.
References transform().
Referenced by ParticleNames::_particleId(), and AnalysisHandler::init().
00040 { 00041 string out = s; 00042 std::transform(out.begin(), out.end(), out.begin(), (int(*)(int)) toupper); 00043 return out; 00044 }
| double Rivet::trace | ( | const Matrix< N > & | m | ) | [inline] |
Definition at line 358 of file MatrixN.hh.
References Matrix< N >::trace().
00358 { 00359 return m.trace(); 00360 }
| FourVector transform | ( | const LorentzTransform & | lt, | |
| const FourVector & | v4 | |||
| ) | [inline] |
| Matrix<N> Rivet::transpose | ( | const Matrix< N > & | m | ) | [inline] |
Definition at line 336 of file MatrixN.hh.
References Matrix< N >::transpose().
00336 { 00337 // Matrix<N> tmp; 00338 // for (size_t i = 0; i < N; ++i) { 00339 // for (size_t j = 0; j < N; ++j) { 00340 // tmp.set(i, j, m.get(j, i)); 00341 // } 00342 // } 00343 // return tmp; 00344 return m.transpose(); 00345 }
| Vector<2> Rivet::unit | ( | const Vector< 2 > & | v | ) | [inline] |
Definition at line 53 of file Spherocity.cc.
References mod(), and Vector< N >::set().
Referenced by Spherocity::_calcSpherocity(), and Thrust::_calcThrust().
| string version | ( | ) |
| vector<GenVertex*> Rivet::vertices | ( | const GenEvent * | ge | ) | [inline] |
Definition at line 46 of file RivetHepMC.hh.
References vertices().
00046 { 00047 assert(ge); 00048 return vertices(*ge); 00049 }
| vector<GenVertex*> Rivet::vertices | ( | const GenEvent & | ge | ) | [inline] |
Definition at line 39 of file RivetHepMC.hh.
Referenced by vertices().
Variable Documentation
const double alpha_rcl2 [static] |
Definition at line 71 of file Constants.hh.
Definition at line 53 of file Constants.hh.
Definition at line 52 of file Constants.hh.
Definition at line 21 of file ParticleName.hh.
Referenced by MC_SUSY::analyze(), CDF_2008_S8095620::init(), CDF_2006_S6653332::init(), and ParticleNames::ParticleNames().
const PdgId ANTINEUTRON = -2112 [static] |
Definition at line 19 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames().
const PdgId ANTIPROTON = -2212 [static] |
Definition at line 16 of file ParticleName.hh.
Referenced by ParticleNames::_particleId(), CDF_1988_S1865951::CDF_1988_S1865951(), CDF_1990_S2089246::CDF_1990_S2089246(), CDF_1993_S2742446::CDF_1993_S2742446(), CDF_1994_S2952106::CDF_1994_S2952106(), CDF_1996_S3108457::CDF_1996_S3108457(), CDF_1996_S3349578::CDF_1996_S3349578(), CDF_1996_S3418421::CDF_1996_S3418421(), CDF_1997_S3541940::CDF_1997_S3541940(), CDF_1998_S3618439::CDF_1998_S3618439(), CDF_2000_S4155203::CDF_2000_S4155203(), CDF_2000_S4266730::CDF_2000_S4266730(), CDF_2001_S4517016::CDF_2001_S4517016(), CDF_2001_S4563131::CDF_2001_S4563131(), CDF_2001_S4751469::CDF_2001_S4751469(), CDF_2002_S4796047::CDF_2002_S4796047(), CDF_2004_S5839831::CDF_2004_S5839831(), CDF_2005_S6080774::CDF_2005_S6080774(), CDF_2005_S6217184::CDF_2005_S6217184(), CDF_2006_S6450792::CDF_2006_S6450792(), CDF_2006_S6653332::CDF_2006_S6653332(), CDF_2007_S7057202::CDF_2007_S7057202(), CDF_2008_LEADINGJETS::CDF_2008_LEADINGJETS(), CDF_2008_NOTE_9351::CDF_2008_NOTE_9351(), CDF_2008_S7540469::CDF_2008_S7540469(), CDF_2008_S7541902::CDF_2008_S7541902(), CDF_2008_S7782535::CDF_2008_S7782535(), CDF_2008_S7828950::CDF_2008_S7828950(), CDF_2008_S8093652::CDF_2008_S8093652(), CDF_2008_S8095620::CDF_2008_S8095620(), CDF_2009_NOTE_9936::CDF_2009_NOTE_9936(), CDF_2009_S8057893::CDF_2009_S8057893::CDF_2009_S8057893(), CDF_2009_S8233977::CDF_2009_S8233977(), CDF_2009_S8383952::CDF_2009_S8383952(), CDF_2009_S8436959::CDF_2009_S8436959(), CDF_2010_S8591881_DY::CDF_2010_S8591881_DY(), CDF_2010_S8591881_QCD::CDF_2010_S8591881_QCD(), D0_1996_S3214044::D0_1996_S3214044(), D0_1996_S3324664::D0_1996_S3324664(), D0_2001_S4674421::D0_2001_S4674421(), D0_2004_S5992206::D0_2004_S5992206(), D0_2006_S6438750::D0_2006_S6438750(), D0_2007_S7075677::D0_2007_S7075677(), D0_2008_S6879055::D0_2008_S6879055(), D0_2008_S7554427::D0_2008_S7554427(), D0_2008_S7662670::D0_2008_S7662670(), D0_2008_S7719523::D0_2008_S7719523(), D0_2008_S7837160::D0_2008_S7837160(), D0_2008_S7863608::D0_2008_S7863608(), D0_2009_S8202443::D0_2009_S8202443(), D0_2009_S8320160::D0_2009_S8320160(), D0_2009_S8349509::D0_2009_S8349509(), D0_2010_S8566488::D0_2010_S8566488(), D0_2010_S8570965::D0_2010_S8570965(), D0_2010_S8671338::D0_2010_S8671338(), E735_1998_S3905616::E735_1998_S3905616(), ParticleNames::ParticleNames(), UA1_1990_S2044935::UA1_1990_S2044935(), UA5_1986_S1583476::UA5_1986_S1583476(), UA5_1987_S1640666::UA5_1987_S1640666(), UA5_1988_S1867512::UA5_1988_S1867512(), and UA5_1989_S1926373::UA5_1989_S1926373().
Definition at line 41 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames().
Definition at line 58 of file ParticleName.hh.
Referenced by compatible(), AnalysisInfo::make(), ParticleNames::ParticleNames(), and Projection::Projection().
const double atmosphere = 101325*pascal [static] |
const double Avogadro = 6.0221367e+23/mole [static] |
Definition at line 20 of file Constants.hh.
const double Bohr_radius = electron_Compton_length/fine_structure_const [static] |
Definition at line 69 of file Constants.hh.
Definition at line 56 of file ParticleName.hh.
Referenced by OPAL_1998_S3780481::analyze(), CDF_2008_S8095620::analyze(), CDF_2006_S6653332::analyze(), and Jet::containsBottom().
const double c_light = 2.99792458e+8 * m/s [static] |
Definition at line 26 of file Constants.hh.
Definition at line 27 of file Constants.hh.
const double centimeter = 10.*millimeter [static] |
const double centimeter2 = centimeter*centimeter [static] |
const double centimeter3 = centimeter*centimeter*centimeter [static] |
const double classic_electr_radius = elm_coupling/electron_mass_c2 [static] |
Definition at line 67 of file Constants.hh.
const double cm = centimeter [static] |
Definition at line 42 of file Units.hh.
Referenced by ExampleAnalysis::analyze().
const double cm2 = centimeter2 [static] |
const double cm3 = centimeter3 [static] |
Definition at line 55 of file ParticleName.hh.
Referenced by OPAL_1998_S3780481::analyze(), and Jet::containsCharm().
Definition at line 72 of file Units.hh.
Referenced by D0_1996_S3214044::_fourJetAnalysis(), D0_1996_S3214044::_threeJetAnalysis(), H1_2000_S4129130::analyze(), H1_1994_S2919893::analyze(), and H1_1994_S2919893::beamAngle().
Definition at line 52 of file ParticleName.hh.
Referenced by OPAL_1998_S3780481::analyze().
Definition at line 43 of file Constants.hh.
Definition at line 13 of file ParticleName.hh.
Referenced by WFinder::_init(), ParticleNames::_particleId(), IdentifiedFinalState::acceptChLeptons(), ALEPH_1991_S2435284::ALEPH_1991_S2435284(), ALEPH_1996_S3196992::ALEPH_1996_S3196992(), ALEPH_1996_S3486095::ALEPH_1996_S3486095(), ALEPH_2004_S5765862::ALEPH_2004_S5765862(), MC_SUSY::analyze(), CDF_2008_S7541902::analyze(), BELLE_2006_S6265367::BELLE_2006_S6265367(), DELPHI_1995_S3137023::DELPHI_1995_S3137023(), DELPHI_1996_S3430090::DELPHI_1996_S3430090(), DELPHI_2002_069_CONF_603::DELPHI_2002_069_CONF_603(), H1_1994_S2919893::H1_1994_S2919893(), H1_1995_S3167097::H1_1995_S3167097(), MC_ZZJETS::init(), MC_ZJETS::init(), MC_WWJETS::init(), MC_WPOL::init(), MC_WJETS::init(), MC_SUSY::init(), D0_2010_S8821313::init(), D0_2009_S8202443::init(), D0_2008_S7837160::init(), D0_2008_S7554427::init(), D0_2008_S6879055::init(), D0_2007_S7075677::init(), D0_2001_S4674421::init(), D0_2000_S4480767::init(), CDF_2009_S8383952::init(), CDF_2008_S8095620::init(), CDF_2008_S7541902::init(), CDF_2008_S7540469::init(), CDF_2006_S6653332::init(), CDF_2000_S4155203::init(), ATLAS_2011_S9019561::init(), ATLAS_2011_S8983313::init(), ATLAS_2011_CONF_2011_090::init(), ATLAS_2010_S8919674::init(), JADE_1998_S3612880::JADE_1998_S3612880(), JADE_OPAL_2000_S4300807::JADE_OPAL_2000_S4300807(), OPAL_1993_S2692198::OPAL_1993_S2692198(), OPAL_1998_S3780481::OPAL_1998_S3780481(), OPAL_2001_S4553896::OPAL_2001_S4553896(), ParticleNames::ParticleNames(), PDG_HADRON_MULTIPLICITIES::PDG_HADRON_MULTIPLICITIES(), PDG_HADRON_MULTIPLICITIES_RATIOS::PDG_HADRON_MULTIPLICITIES_RATIOS(), InitialQuarks::project(), and TASSO_1990_S2148048::TASSO_1990_S2148048().
const double electron_charge = - eplus [static] |
Definition at line 42 of file Constants.hh.
const double electron_Compton_length = hbarc/electron_mass_c2 [static] |
Definition at line 68 of file Constants.hh.
const double electron_mass_c2 = 0.51099906 * MeV [static] |
Definition at line 49 of file Constants.hh.
const double electronvolt = 1.e-9*gigaelectronvolt [static] |
const double elm_coupling = e_squared/(4*pi*epsilon0) [static] |
Definition at line 65 of file Constants.hh.
Definition at line 42 of file ParticleName.hh.
Definition at line 43 of file ParticleName.hh.
const double eplus = 1.0 [static] |
Definition at line 102 of file Units.hh.
Referenced by D0_2010_S8821313::analyze().
Definition at line 60 of file Constants.hh.
const double eV = electronvolt [static] |
const double femtobarn = 1.0e-15 * barn [static] |
Definition at line 64 of file Units.hh.
Referenced by CDF_2008_S7540469::finalize().
const double femtometer = 1.e-15*meter [static] |
const double fermi = femtometer [static] |
const double fine_structure_const = elm_coupling/hbarc [static] |
Definition at line 66 of file Constants.hh.
Definition at line 47 of file ParticleName.hh.
const double GeV = gigaelectronvolt [static] |
Definition at line 121 of file Units.hh.
Referenced by CDF_2004_S5839831::_calcTransCones(), CDF_1996_S3349578::_fiveJetAnalysis(), D0_1996_S3214044::_fourJetAnalysis(), CDF_1996_S3349578::_fourJetAnalysis(), Event::_geNormAlignment(), D0_1996_S3214044::_threeJetAnalysis(), CDF_1996_S3349578::_threeJetAnalysis(), UA1_1990_S2044935::analyze(), TASSO_1990_S2148048::analyze(), STAR_2008_S7993412::analyze(), STAR_2008_S7869363::analyze(), STAR_2006_S6860818::analyze(), STAR_2006_S6500200::analyze(), PDG_HADRON_MULTIPLICITIES_RATIOS::analyze(), PDG_HADRON_MULTIPLICITIES::analyze(), OPAL_2001_S4553896::analyze(), MC_ZZJETS::analyze(), MC_ZJETS::analyze(), MC_WWJETS::analyze(), MC_WPOL::analyze(), MC_WJETS::analyze(), MC_TTBAR::analyze(), MC_SUSY::analyze(), MC_PHOTONJETUE::analyze(), MC_PHOTONJETS::analyze(), MC_LEADINGJETS::analyze(), MC_JetAnalysis::analyze(), MC_HJETS::analyze(), MC_GENERIC::analyze(), MC_DIPHOTON::analyze(), MC_DIJET::analyze(), JADE_1998_S3612880::analyze(), H1_2000_S4129130::analyze(), H1_1995_S3167097::analyze(), H1_1994_S2919893::analyze(), ExampleAnalysis::analyze(), DELPHI_1996_S3430090::analyze(), D0_2010_S8671338::analyze(), D0_2010_S8570965::analyze(), D0_2010_S8566488::analyze(), D0_2009_S8349509::analyze(), D0_2009_S8202443::analyze(), D0_2008_S7863608::analyze(), D0_2008_S7837160::analyze(), D0_2008_S7719523::analyze(), D0_2008_S7662670::analyze(), D0_2008_S6879055::analyze(), D0_2007_S7075677::analyze(), D0_2004_S5992206::analyze(), D0_2001_S4674421::analyze(), D0_2000_S4480767::analyze(), D0_1996_S3324664::analyze(), D0_1996_S3214044::analyze(), CMS_2011_S8957746::analyze(), CDF_2010_S8591881_QCD::analyze(), CDF_2010_S8591881_DY::analyze(), CDF_2009_S8436959::analyze(), CDF_2009_S8233977::analyze(), CDF_2008_S7828950::analyze(), CDF_2008_S7782535::analyze(), CDF_2008_S7540469::analyze(), CDF_2008_NOTE_9351::analyze(), CDF_2008_LEADINGJETS::analyze(), CDF_2007_S7057202::analyze(), CDF_2006_S6450792::analyze(), CDF_2005_S6217184::analyze(), CDF_2005_S6080774::analyze(), CDF_2004_S5839831::analyze(), CDF_2002_S4796047::analyze(), CDF_2001_S4751469::analyze(), CDF_2001_S4563131::analyze(), CDF_2001_S4517016::analyze(), CDF_2000_S4266730::analyze(), CDF_2000_S4155203::analyze(), CDF_1998_S3618439::analyze(), CDF_1997_S3541940::analyze(), CDF_1996_S3418421::analyze(), CDF_1996_S3349578::analyze(), CDF_1996_S3108457::analyze(), CDF_1994_S2952106::analyze(), CDF_1993_S2742446::analyze(), CDF_1988_S1865951::analyze(), ATLAS_2011_S9120807::analyze(), ATLAS_2011_S9019561::analyze(), ATLAS_2011_S9002537::analyze(), ATLAS_2011_S8994773::analyze(), ATLAS_2011_S8983313::analyze(), ATLAS_2011_S8971293::analyze(), ATLAS_2011_S8924791::analyze(), ATLAS_2011_CONF_2011_090::analyze(), ATLAS_2010_S8919674::analyze(), ATLAS_2010_S8918562::analyze(), ATLAS_2010_S8914702::analyze(), ATLAS_2010_S8894728::analyze(), ATLAS_2010_S8817804::analyze(), ATLAS_2010_S8591806::analyze(), ATLAS_2010_CONF_2010_049::analyze(), AnalysisHandler::analyze(), ALICE_2010_S8706239::analyze(), ALICE_2010_S8625980::analyze(), ALEPH_2004_S5765862::analyze(), ALEPH_1996_S3486095::analyze(), ALEPH_1996_S3196992::analyze(), InvMassFinalState::calc(), CDF_2009_S8057893::CDF_2009_S8057893::init(), ATLAS_2010_S8918562::fillPtEtaNch(), UA1_1990_S2044935::finalize(), PDG_HADRON_MULTIPLICITIES_RATIOS::finalize(), PDG_HADRON_MULTIPLICITIES::finalize(), JADE_1998_S3612880::finalize(), CMS_2011_S8978280::finalize(), CDF_2004_S5839831::finalize(), CDF_2002_S4796047::finalize(), ATLAS_2010_S8918562::finalize(), ALICE_2010_S8625980::finalize(), OPAL_2004_S6132243::getHistIndex(), UA5_1989_S1926373::init(), UA5_1988_S1867512::init(), UA5_1986_S1583476::init(), UA1_1990_S2044935::init(), TASSO_1990_S2148048::init(), STAR_2009_UE_HELEN::init(), STAR_2008_S7993412::init(), STAR_2008_S7869363::init(), STAR_2006_S6860818::init(), STAR_2006_S6500200::init(), SFM_1984_S1178091::init(), PDG_HADRON_MULTIPLICITIES_RATIOS::init(), PDG_HADRON_MULTIPLICITIES::init(), MC_ZZJETS::init(), MC_ZJETS::init(), MC_WWJETS::init(), MC_WPOL::init(), MC_WJETS::init(), MC_TTBAR::init(), MC_SUSY::init(), MC_PHOTONJETUE::init(), MC_PHOTONJETS::init(), MC_LEADINGJETS::init(), MC_JetAnalysis::init(), MC_HJETS::init(), MC_DIPHOTON::init(), MC_DIJET::init(), JADE_OPAL_2000_S4300807::init(), JADE_1998_S3612880::init(), ExampleAnalysis::init(), D0_2010_S8821313::init(), D0_2010_S8671338::init(), D0_2010_S8570965::init(), D0_2009_S8349509::init(), D0_2009_S8202443::init(), D0_2008_S7863608::init(), D0_2008_S7837160::init(), D0_2008_S7719523::init(), D0_2008_S7554427::init(), D0_2008_S6879055::init(), D0_2007_S7075677::init(), D0_2006_S6438750::init(), D0_2004_S5992206::init(), D0_2000_S4480767::init(), CMS_2011_S8978280::init(), CMS_2011_S8957746::init(), CMS_2011_S8884919::init(), CMS_2010_S8656010::init(), CMS_2010_S8547297::init(), CDF_2010_S8591881_QCD::init(), CDF_2010_S8591881_DY::init(), CDF_2009_S8436959::init(), CDF_2009_S8383952::init(), CDF_2009_S8233977::init(), CDF_2009_NOTE_9936::init(), CDF_2008_S8095620::init(), CDF_2008_S7541902::init(), CDF_2008_S7540469::init(), CDF_2008_NOTE_9351::init(), CDF_2008_LEADINGJETS::init(), CDF_2006_S6653332::init(), CDF_2005_S6080774::init(), CDF_2004_S5839831::init(), CDF_2002_S4796047::init(), CDF_2001_S4751469::init(), CDF_2000_S4155203::init(), CDF_1993_S2742446::init(), CDF_1990_S2089246::init(), CDF_1988_S1865951::init(), ATLAS_2011_S9120807::init(), ATLAS_2011_S9019561::init(), ATLAS_2011_S9002537::init(), ATLAS_2011_S8994773::init(), ATLAS_2011_S8983313::init(), ATLAS_2011_CONF_2011_090::init(), ATLAS_2010_S8919674::init(), ATLAS_2010_S8918562::init(), ATLAS_2010_S8914702::init(), ATLAS_2010_S8894728::init(), ATLAS_2010_S8591806::init(), ATLAS_2010_CONF_2010_049::init(), ALICE_2010_S8625980::init(), ALICE_2010_S8624100::init(), ALEPH_2004_S5765862::init(), NeutralFinalState::NeutralFinalState(), WFinder::project(), AnalysisHandler::setRunBeams(), and toString().
Definition at line 128 of file Units.hh.
Referenced by H1_1995_S3167097::_getbin(), H1_2000_S4129130::analyze(), H1_1995_S3167097::analyze(), H1_1994_S2919893::analyze(), and CDF_2000_S4155203::analyze().
const double gigaelectronvolt = 1. [static] |
Definition at line 46 of file ParticleName.hh.
const double h_Planck = 6.6260755e-34 * joule*s [static] |
Definition at line 34 of file Constants.hh.
| const double HALFPI = M_PI_2 |
A pre-defined value of 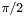 .
.
Definition at line 51 of file MathHeader.hh.
Definition at line 14 of file Constants.hh.
const double hbar_Planck = h_Planck/twopi [static] |
Definition at line 35 of file Constants.hh.
const double hbarc = hbar_Planck * c_light [static] |
Definition at line 36 of file Constants.hh.
const double hbarc_squared = hbarc * hbarc [static] |
Definition at line 37 of file Constants.hh.
const double hep_pascal = newton/m2 [static] |
Definition at line 51 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames().
const double joule = electronvolt/e_SI [static] |
Definition at line 30 of file ParticleName.hh.
Referenced by STAR_2006_S6860818::analyze(), and STAR_2009_UE_HELEN::init().
Definition at line 31 of file ParticleName.hh.
Referenced by STAR_2006_S6860818::analyze(), and CMS_2011_S8978280::analyze().
const double k_Boltzmann = 8.617385e-11 * MeV/kelvin [static] |
Definition at line 81 of file Constants.hh.
const double keV = kiloelectronvolt [static] |
const double kGasThreshold = 10.*mg/cm3 [static] |
Definition at line 88 of file Constants.hh.
const double kiloelectronvolt = 1.e-6*gigaelectronvolt [static] |
const double kilometer2 = kilometer*kilometer [static] |
const double kilometer3 = kilometer*kilometer*kilometer [static] |
const double km2 = kilometer2 [static] |
const double km3 = kilometer3 [static] |
Definition at line 33 of file ParticleName.hh.
Definition at line 32 of file ParticleName.hh.
Referenced by STAR_2006_S6860818::analyze().
Definition at line 34 of file ParticleName.hh.
Referenced by STAR_2006_S6860818::analyze(), and CMS_2011_S8978280::analyze().
Definition at line 35 of file ParticleName.hh.
Definition at line 46 of file Units.hh.
Referenced by CDF_1996_S3418421::analyze(), ALEPH_1991_S2435284::analyze(), and operator<<().
Definition at line 47 of file Units.hh.
Referenced by D0_1996_S3214044::_safeMass(), CDF_1997_S3541940::_safeMass(), CDF_1996_S3349578::_safeMass(), MC_ZZJETS::analyze(), and MC_WWJETS::analyze().
| const double MAXDOUBLE = std::numeric_limits<double>::max() |
Definition at line 41 of file MathHeader.hh.
Referenced by D0_2004_S5992206::init(), and rapidity().
| const double MAXINT = std::numeric_limits<int>::max() |
Definition at line 42 of file MathHeader.hh.
const double MaxRapidity = 100000.0 [static] |
const double MAXRAPIDITY = 100000.0 [static] |
A sensible default maximum value of rapidity for Rivet analyses to use.
Definition at line 24 of file Rivet.hh.
Referenced by FinalState::FinalState(), TASSO_1990_S2148048::init(), MC_WPOL::init(), JADE_1998_S3612880::init(), D0_2009_S8202443::init(), D0_2008_S7554427::init(), D0_2008_S6879055::init(), D0_2007_S7075677::init(), CDF_2009_S8383952::init(), CDF_2000_S4155203::init(), and ALEPH_1996_S3196992::init().
const double megaelectronvolt = 1.e-3*gigaelectronvolt [static] |
const double megavolt = megaelectronvolt/eplus [static] |
const double meter = 1000.*millimeter [static] |
const double MeV = megaelectronvolt [static] |
Definition at line 120 of file Units.hh.
Referenced by CMS_2011_S8957746::analyze(), CDF_2009_S8233977::analyze(), MC_GENERIC::init(), ATLAS_2011_S8994773::init(), ATLAS_2010_S8918562::init(), ATLAS_2010_S8894728::init(), and STARRandomFilter::operator()().
const double microampere = 1.e-6*ampere [static] |
const double microbarn = 1.0e-6 * barn [static] |
Definition at line 62 of file Units.hh.
Referenced by ATLAS_2010_CONF_2010_049::finalize().
const double microfarad = 1.e-6*farad [static] |
const double micrometer = 1.e-6 *meter [static] |
const double microsecond = 1.e-6 *second [static] |
const double milliampere = 1.e-3*ampere [static] |
const double millibarn = 1.0e-3 * barn [static] |
Definition at line 61 of file Units.hh.
Referenced by UA1_1990_S2044935::finalize(), CDF_2009_S8233977::finalize(), and CDF_1988_S1865951::finalize().
const double millifarad = 1.e-3*farad [static] |
const double millimeter = 1. [static] |
const double millimeter2 = millimeter*millimeter [static] |
const double millimeter3 = millimeter*millimeter*millimeter [static] |
const double milliradian = 1.e-3*radian [static] |
const double millisecond = 1.e-3 *second [static] |
const double mm = millimeter [static] |
Definition at line 38 of file Units.hh.
Referenced by MC_ZZJETS::analyze(), MC_WWJETS::analyze(), and D0_2010_S8821313::analyze().
const double mm2 = millimeter2 [static] |
const double mm3 = millimeter3 [static] |
const double mrad = milliradian [static] |
const double ms = millisecond [static] |
Definition at line 20 of file ParticleName.hh.
Referenced by WFinder::_init(), IdentifiedFinalState::acceptChLeptons(), MC_SUSY::analyze(), MC_ZZJETS::init(), MC_WWJETS::init(), MC_SUSY::init(), D0_2010_S8821313::init(), D0_2010_S8671338::init(), D0_2009_S8349509::init(), D0_2008_S7863608::init(), D0_2004_S5992206::init(), CDF_2008_S8095620::init(), CDF_2006_S6653332::init(), ATLAS_2011_S9019561::init(), ATLAS_2011_S9002537::init(), ATLAS_2011_S8983313::init(), ATLAS_2011_CONF_2011_090::init(), ATLAS_2010_S8919674::init(), and ParticleNames::ParticleNames().
const double nanoampere = 1.e-9*ampere [static] |
const double nanobarn = 1.0e-9 * barn [static] |
Definition at line 63 of file Units.hh.
Referenced by CDF_2008_S7828950::finalize(), CDF_2007_S7057202::finalize(), CDF_2006_S6450792::finalize(), CDF_2001_S4563131::finalize(), and CDF_2001_S4517016::finalize().
const double nanosecond = 1.0 [static] |
Definition at line 18 of file ParticleName.hh.
Referenced by ParticleNames::_particleId(), STAR_2009_UE_HELEN::init(), and ParticleNames::ParticleNames().
const double neutron_mass_c2 = 939.56563 * MeV [static] |
Definition at line 51 of file Constants.hh.
const double ns = nanosecond [static] |
Definition at line 22 of file ParticleName.hh.
Referenced by WFinder::_init(), IdentifiedFinalState::acceptNeutrinos(), CDF_2008_S7541902::analyze(), D0_2001_S4674421::init(), CDF_2008_S7541902::init(), ATLAS_2010_S8919674::init(), ParticleNames::ParticleNames(), and VetoedFinalState::vetoNeutrinos().
Definition at line 23 of file ParticleName.hh.
Referenced by D0_2001_S4674421::init(), CDF_2008_S7541902::init(), and ParticleNames::ParticleNames().
Definition at line 24 of file ParticleName.hh.
Referenced by WFinder::_init(), IdentifiedFinalState::acceptNeutrinos(), ATLAS_2010_S8919674::init(), ParticleNames::ParticleNames(), and VetoedFinalState::vetoNeutrinos().
Definition at line 25 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames().
Definition at line 26 of file ParticleName.hh.
Referenced by IdentifiedFinalState::acceptNeutrinos(), ParticleNames::ParticleNames(), and VetoedFinalState::vetoNeutrinos().
Definition at line 27 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames().
const PdgId OMEGAMINUS = 3334 [static] |
Definition at line 38 of file ParticleName.hh.
Referenced by STAR_2006_S6860818::analyze().
Definition at line 39 of file ParticleName.hh.
Definition at line 44 of file ParticleName.hh.
Definition at line 45 of file ParticleName.hh.
const double perMillion = 0.000001 [static] |
const double perThousand = 0.001 [static] |
const double petaelectronvolt = 1.e+6*gigaelectronvolt [static] |
const double PeV = petaelectronvolt [static] |
Definition at line 17 of file ParticleName.hh.
Referenced by ParticleNames::_particleId(), OPAL_1993_S2692198::analyze(), CDF_2008_S7540469::analyze(), ClusteredPhotons::ClusteredPhotons(), MC_SUSY::init(), MC_PHOTONJETUE::init(), MC_PHOTONJETS::init(), MC_DIPHOTON::init(), D0_2010_S8570965::init(), D0_2008_S7719523::init(), D0_2006_S6438750::init(), CDF_2009_S8436959::init(), CDF_2005_S6080774::init(), CDF_1993_S2742446::init(), ATLAS_2011_S9120807::init(), ATLAS_2010_S8914702::init(), ALEPH_1996_S3196992::init(), LeptonClusters::LeptonClusters(), and ParticleNames::ParticleNames().
| const double PI = M_PI |
A pre-defined value of  .
.
Definition at line 45 of file MathHeader.hh.
Referenced by Spherocity::_calcSpherocity(), CDF_2004_S5839831::_calcTransCones(), STAR_2009_UE_HELEN::analyze(), MC_PHOTONJETUE::analyze(), MC_LEADINGJETS::analyze(), H1_1994_S2919893::analyze(), CDF_2010_S8591881_QCD::analyze(), CDF_2010_S8591881_DY::analyze(), CDF_2008_NOTE_9351::analyze(), CDF_2008_LEADINGJETS::analyze(), CDF_2001_S4751469::analyze(), CDF_1994_S2952106::analyze(), ATLAS_2011_S9120807::analyze(), ATLAS_2011_S8994773::analyze(), ATLAS_2010_S8914702::analyze(), ATLAS_2010_S8894728::analyze(), Vector3::azimuthalAngle(), MC_ZZJETS::init(), MC_WWJETS::init(), MC_SUSY::init(), MC_PHOTONJETUE::init(), mapAngle0ToPi(), mapAngleMPiToPi(), Vector3::polarAngle(), DISKinematics::project(), ATLAS_2011_S8994773::region_index(), and ATLAS_2010_S8894728::region_index().
const double pi = 3.14159265358979323846 [static] |
Definition at line 12 of file Constants.hh.
Referenced by Jet::containsBottom(), Jet::containsCharm(), particles(), FoxWolframMoments::project(), and ProjectionHandler::removeProjectionApplier().
Definition at line 15 of file Constants.hh.
const double picobarn = 1.0 [static] |
Definition at line 59 of file Units.hh.
Referenced by STAR_2006_S6870392::finalize(), D0_2001_S4674421::finalize(), CDF_2000_S4266730::finalize(), CDF_2000_S4155203::finalize(), CDF_1998_S3618439::finalize(), and ATLAS_2010_S8817804::finalize().
const double picosecond = 1.e-12*second [static] |
Definition at line 29 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames().
Definition at line 28 of file ParticleName.hh.
Referenced by STAR_2006_S6860818::analyze(), STAR_2006_S6500200::init(), and ParticleNames::ParticleNames().
| AnalysisBuilder<ALEPH_1991_S2435284> plugin_ALEPH_1991_S2435284 |
Definition at line 64 of file ALEPH_1991_S2435284.cc.
| AnalysisBuilder<ALEPH_1996_S3196992> plugin_ALEPH_1996_S3196992 |
Definition at line 166 of file ALEPH_1996_S3196992.cc.
| AnalysisBuilder<ALEPH_1996_S3486095> plugin_ALEPH_1996_S3486095 |
Definition at line 560 of file ALEPH_1996_S3486095.cc.
| AnalysisBuilder<ALEPH_2004_S5765862> plugin_ALEPH_2004_S5765862 |
Definition at line 326 of file ALEPH_2004_S5765862.cc.
| AnalysisBuilder<ALICE_2010_S8624100> plugin_ALICE_2010_S8624100 |
Definition at line 98 of file ALICE_2010_S8624100.cc.
| AnalysisBuilder<ALICE_2010_S8625980> plugin_ALICE_2010_S8625980 |
Definition at line 103 of file ALICE_2010_S8625980.cc.
| AnalysisBuilder<ALICE_2010_S8706239> plugin_ALICE_2010_S8706239 |
Definition at line 104 of file ALICE_2010_S8706239.cc.
| AnalysisBuilder<ATLAS_2010_CONF_2010_049> plugin_ATLAS_2010_CONF_2010_049 |
Definition at line 123 of file ATLAS_2010_CONF_2010_049.cc.
| AnalysisBuilder<ATLAS_2010_S8591806> plugin_ATLAS_2010_S8591806 |
Definition at line 75 of file ATLAS_2010_S8591806.cc.
| AnalysisBuilder<ATLAS_2010_S8817804> plugin_ATLAS_2010_S8817804 |
Definition at line 123 of file ATLAS_2010_S8817804.cc.
| AnalysisBuilder<ATLAS_2010_S8894728> plugin_ATLAS_2010_S8894728 |
Definition at line 332 of file ATLAS_2010_S8894728.cc.
| AnalysisBuilder<ATLAS_2010_S8914702> plugin_ATLAS_2010_S8914702 |
Definition at line 202 of file ATLAS_2010_S8914702.cc.
| AnalysisBuilder<ATLAS_2010_S8918562> plugin_ATLAS_2010_S8918562 |
Definition at line 220 of file ATLAS_2010_S8918562.cc.
| AnalysisBuilder<ATLAS_2010_S8919674> plugin_ATLAS_2010_S8919674 |
Definition at line 203 of file ATLAS_2010_S8919674.cc.
| AnalysisBuilder<ATLAS_2011_CONF_2011_090> plugin_ATLAS_2011_CONF_2011_090 |
Definition at line 377 of file ATLAS_2011_CONF_2011_090.cc.
| AnalysisBuilder<ATLAS_2011_S8924791> plugin_ATLAS_2011_S8924791 |
Definition at line 131 of file ATLAS_2011_S8924791.cc.
| AnalysisBuilder<ATLAS_2011_S8971293> plugin_ATLAS_2011_S8971293 |
Definition at line 94 of file ATLAS_2011_S8971293.cc.
| AnalysisBuilder<ATLAS_2011_S8983313> plugin_ATLAS_2011_S8983313 |
Definition at line 332 of file ATLAS_2011_S8983313.cc.
| AnalysisBuilder<ATLAS_2011_S8994773> plugin_ATLAS_2011_S8994773 |
Definition at line 136 of file ATLAS_2011_S8994773.cc.
| AnalysisBuilder<ATLAS_2011_S9002537> plugin_ATLAS_2011_S9002537 |
Definition at line 107 of file ATLAS_2011_S9002537.cc.
| AnalysisBuilder<ATLAS_2011_S9019561> plugin_ATLAS_2011_S9019561 |
Definition at line 336 of file ATLAS_2011_S9019561.cc.
| AnalysisBuilder<ATLAS_2011_S9120807> plugin_ATLAS_2011_S9120807 |
Definition at line 240 of file ATLAS_2011_S9120807.cc.
| AnalysisBuilder<BELLE_2006_S6265367> plugin_BELLE_2006_S6265367 |
Definition at line 219 of file BELLE_2006_S6265367.cc.
| AnalysisBuilder<CDF_1988_S1865951> plugin_CDF_1988_S1865951 |
Definition at line 86 of file CDF_1988_S1865951.cc.
| AnalysisBuilder<CDF_1990_S2089246> plugin_CDF_1990_S2089246 |
Definition at line 86 of file CDF_1990_S2089246.cc.
| AnalysisBuilder<CDF_1993_S2742446> plugin_CDF_1993_S2742446 |
Definition at line 103 of file CDF_1993_S2742446.cc.
| AnalysisBuilder<CDF_1994_S2952106> plugin_CDF_1994_S2952106 |
Definition at line 217 of file CDF_1994_S2952106.cc.
| AnalysisBuilder<CDF_1996_S3108457> plugin_CDF_1996_S3108457 |
Definition at line 131 of file CDF_1996_S3108457.cc.
| AnalysisBuilder<CDF_1996_S3349578> plugin_CDF_1996_S3349578 |
Definition at line 472 of file CDF_1996_S3349578.cc.
| AnalysisBuilder<CDF_1996_S3418421> plugin_CDF_1996_S3418421 |
Definition at line 124 of file CDF_1996_S3418421.cc.
| AnalysisBuilder<CDF_1997_S3541940> plugin_CDF_1997_S3541940 |
Definition at line 275 of file CDF_1997_S3541940.cc.
| AnalysisBuilder<CDF_1998_S3618439> plugin_CDF_1998_S3618439 |
Definition at line 81 of file CDF_1998_S3618439.cc.
| AnalysisBuilder<CDF_2000_S4155203> plugin_CDF_2000_S4155203 |
Definition at line 76 of file CDF_2000_S4155203.cc.
| AnalysisBuilder<CDF_2000_S4266730> plugin_CDF_2000_S4266730 |
Definition at line 89 of file CDF_2000_S4266730.cc.
| AnalysisBuilder<CDF_2001_S4517016> plugin_CDF_2001_S4517016 |
Definition at line 93 of file CDF_2001_S4517016.cc.
| AnalysisBuilder<CDF_2001_S4563131> plugin_CDF_2001_S4563131 |
Definition at line 80 of file CDF_2001_S4563131.cc.
| AnalysisBuilder<CDF_2001_S4751469> plugin_CDF_2001_S4751469 |
Definition at line 289 of file CDF_2001_S4751469.cc.
| AnalysisBuilder<CDF_2002_S4796047> plugin_CDF_2002_S4796047 |
Definition at line 126 of file CDF_2002_S4796047.cc.
| AnalysisBuilder<CDF_2004_S5839831> plugin_CDF_2004_S5839831 |
Definition at line 388 of file CDF_2004_S5839831.cc.
| AnalysisBuilder<CDF_2005_S6080774> plugin_CDF_2005_S6080774 |
Definition at line 107 of file CDF_2005_S6080774.cc.
| AnalysisBuilder<CDF_2005_S6217184> plugin_CDF_2005_S6217184 |
Definition at line 136 of file CDF_2005_S6217184.cc.
| AnalysisBuilder<CDF_2006_S6450792> plugin_CDF_2006_S6450792 |
Definition at line 64 of file CDF_2006_S6450792.cc.
| AnalysisBuilder<CDF_2006_S6653332> plugin_CDF_2006_S6653332 |
Definition at line 188 of file CDF_2006_S6653332.cc.
| AnalysisBuilder<CDF_2007_S7057202> plugin_CDF_2007_S7057202 |
Definition at line 87 of file CDF_2007_S7057202.cc.
| AnalysisBuilder<CDF_2008_LEADINGJETS> plugin_CDF_2008_LEADINGJETS |
Definition at line 236 of file CDF_2008_LEADINGJETS.cc.
| AnalysisBuilder<CDF_2008_NOTE_9351> plugin_CDF_2008_NOTE_9351 |
Definition at line 225 of file CDF_2008_NOTE_9351.cc.
| AnalysisBuilder<CDF_2008_S7540469> plugin_CDF_2008_S7540469 |
Definition at line 197 of file CDF_2008_S7540469.cc.
| AnalysisBuilder<CDF_2008_S7541902> plugin_CDF_2008_S7541902 |
Definition at line 206 of file CDF_2008_S7541902.cc.
| AnalysisBuilder<CDF_2008_S7782535> plugin_CDF_2008_S7782535 |
Definition at line 138 of file CDF_2008_S7782535.cc.
| AnalysisBuilder<CDF_2008_S7828950> plugin_CDF_2008_S7828950 |
Definition at line 72 of file CDF_2008_S7828950.cc.
| AnalysisBuilder<CDF_2008_S8093652> plugin_CDF_2008_S8093652 |
Definition at line 75 of file CDF_2008_S8093652.cc.
| AnalysisBuilder<CDF_2008_S8095620> plugin_CDF_2008_S8095620 |
Definition at line 187 of file CDF_2008_S8095620.cc.
| AnalysisBuilder<CDF_2009_NOTE_9936> plugin_CDF_2009_NOTE_9936 |
Definition at line 79 of file CDF_2009_NOTE_9936.cc.
| AnalysisBuilder<CDF_2009_S8057893> plugin_CDF_2009_S8057893 |
Definition at line 87 of file CDF_2009_S8057893.cc.
| AnalysisBuilder<CDF_2009_S8233977> plugin_CDF_2009_S8233977 |
Definition at line 128 of file CDF_2009_S8233977.cc.
| AnalysisBuilder<CDF_2009_S8383952> plugin_CDF_2009_S8383952 |
Definition at line 93 of file CDF_2009_S8383952.cc.
| AnalysisBuilder<CDF_2009_S8436959> plugin_CDF_2009_S8436959 |
Definition at line 93 of file CDF_2009_S8436959.cc.
| AnalysisBuilder<CDF_2010_S8591881_DY> plugin_CDF_2010_S8591881_DY |
Definition at line 212 of file CDF_2010_S8591881_DY.cc.
| AnalysisBuilder<CDF_2010_S8591881_QCD> plugin_CDF_2010_S8591881_QCD |
Definition at line 196 of file CDF_2010_S8591881_QCD.cc.
| AnalysisBuilder<CMS_2010_S8547297> plugin_CMS_2010_S8547297 |
Definition at line 91 of file CMS_2010_S8547297.cc.
| AnalysisBuilder<CMS_2010_S8656010> plugin_CMS_2010_S8656010 |
Definition at line 82 of file CMS_2010_S8656010.cc.
| AnalysisBuilder<CMS_2011_S8884919> plugin_CMS_2011_S8884919 |
Definition at line 116 of file CMS_2011_S8884919.cc.
| AnalysisBuilder<CMS_2011_S8957746> plugin_CMS_2011_S8957746 |
Definition at line 95 of file CMS_2011_S8957746.cc.
| AnalysisBuilder<CMS_2011_S8968497> plugin_CMS_2011_S8968497 |
Definition at line 51 of file CMS_2011_S8968497.cc.
| AnalysisBuilder<CMS_2011_S8978280> plugin_CMS_2011_S8978280 |
Definition at line 119 of file CMS_2011_S8978280.cc.
| AnalysisBuilder<D0_1996_S3214044> plugin_D0_1996_S3214044 |
Definition at line 278 of file D0_1996_S3214044.cc.
| AnalysisBuilder<D0_1996_S3324664> plugin_D0_1996_S3324664 |
Definition at line 118 of file D0_1996_S3324664.cc.
| AnalysisBuilder<D0_2000_S4480767> plugin_D0_2000_S4480767 |
Definition at line 77 of file D0_2000_S4480767.cc.
| AnalysisBuilder<D0_2001_S4674421> plugin_D0_2001_S4674421 |
Definition at line 189 of file D0_2001_S4674421.cc.
| AnalysisBuilder<D0_2004_S5992206> plugin_D0_2004_S5992206 |
Definition at line 139 of file D0_2004_S5992206.cc.
| AnalysisBuilder<D0_2006_S6438750> plugin_D0_2006_S6438750 |
Definition at line 104 of file D0_2006_S6438750.cc.
| AnalysisBuilder<D0_2007_S7075677> plugin_D0_2007_S7075677 |
Definition at line 79 of file D0_2007_S7075677.cc.
| AnalysisBuilder<D0_2008_S6879055> plugin_D0_2008_S6879055 |
Definition at line 126 of file D0_2008_S6879055.cc.
| AnalysisBuilder<D0_2008_S7554427> plugin_D0_2008_S7554427 |
Definition at line 85 of file D0_2008_S7554427.cc.
| AnalysisBuilder<D0_2008_S7662670> plugin_D0_2008_S7662670 |
Definition at line 128 of file D0_2008_S7662670.cc.
| AnalysisBuilder<D0_2008_S7719523> plugin_D0_2008_S7719523 |
Definition at line 188 of file D0_2008_S7719523.cc.
| AnalysisBuilder<D0_2008_S7837160> plugin_D0_2008_S7837160 |
Definition at line 151 of file D0_2008_S7837160.cc.
| AnalysisBuilder<D0_2008_S7863608> plugin_D0_2008_S7863608 |
Definition at line 139 of file D0_2008_S7863608.cc.
| AnalysisBuilder<D0_2009_S8202443> plugin_D0_2009_S8202443 |
Definition at line 157 of file D0_2009_S8202443.cc.
| AnalysisBuilder<D0_2009_S8320160> plugin_D0_2009_S8320160 |
Definition at line 95 of file D0_2009_S8320160.cc.
| AnalysisBuilder<D0_2009_S8349509> plugin_D0_2009_S8349509 |
Definition at line 175 of file D0_2009_S8349509.cc.
| AnalysisBuilder<D0_2010_S8566488> plugin_D0_2010_S8566488 |
Definition at line 92 of file D0_2010_S8566488.cc.
| AnalysisBuilder<D0_2010_S8570965> plugin_D0_2010_S8570965 |
Definition at line 150 of file D0_2010_S8570965.cc.
| AnalysisBuilder<D0_2010_S8671338> plugin_D0_2010_S8671338 |
Definition at line 74 of file D0_2010_S8671338.cc.
| AnalysisBuilder<D0_2010_S8821313> plugin_D0_2010_S8821313 |
Definition at line 130 of file D0_2010_S8821313.cc.
| AnalysisBuilder<DELPHI_1995_S3137023> plugin_DELPHI_1995_S3137023 |
Definition at line 108 of file DELPHI_1995_S3137023.cc.
| AnalysisBuilder<DELPHI_1996_S3430090> plugin_DELPHI_1996_S3430090 |
Definition at line 551 of file DELPHI_1996_S3430090.cc.
| AnalysisBuilder<DELPHI_2002_069_CONF_603> plugin_DELPHI_2002_069_CONF_603 |
Definition at line 130 of file DELPHI_2002_069_CONF_603.cc.
| AnalysisBuilder<DELPHI_2003_WUD_03_11> plugin_DELPHI_2003_WUD_03_11 |
Definition at line 204 of file DELPHI_2003_WUD_03_11.cc.
| AnalysisBuilder<E735_1998_S3905616> plugin_E735_1998_S3905616 |
Definition at line 76 of file E735_1998_S3905616.cc.
| AnalysisBuilder<ExampleAnalysis> plugin_ExampleAnalysis |
Definition at line 130 of file ExampleAnalysis.cc.
| AnalysisBuilder<H1_1994_S2919893> plugin_H1_1994_S2919893 |
Definition at line 259 of file H1_1994_S2919893.cc.
| AnalysisBuilder<H1_1995_S3167097> plugin_H1_1995_S3167097 |
Definition at line 152 of file H1_1995_S3167097.cc.
| AnalysisBuilder<H1_2000_S4129130> plugin_H1_2000_S4129130 |
Definition at line 281 of file H1_2000_S4129130.cc.
| AnalysisBuilder<JADE_1998_S3612880> plugin_JADE_1998_S3612880 |
Definition at line 134 of file JADE_1998_S3612880.cc.
| AnalysisBuilder<JADE_OPAL_2000_S4300807> plugin_JADE_OPAL_2000_S4300807 |
Definition at line 198 of file JADE_OPAL_2000_S4300807.cc.
| AnalysisBuilder<LHCB_2010_S8758301> plugin_LHCB_2010_S8758301 |
Definition at line 124 of file LHCB_2010_S8758301.cc.
| AnalysisBuilder<MC_DIJET> plugin_MC_DIJET |
Definition at line 118 of file MC_DIJET.cc.
| AnalysisBuilder<MC_DIPHOTON> plugin_MC_DIPHOTON |
Definition at line 108 of file MC_DIPHOTON.cc.
| AnalysisBuilder<MC_GENERIC> plugin_MC_GENERIC |
Definition at line 218 of file MC_GENERIC.cc.
| AnalysisBuilder<MC_HJETS> plugin_MC_HJETS |
Definition at line 116 of file MC_HJETS.cc.
| AnalysisBuilder<MC_JETS> plugin_MC_JETS |
Definition at line 43 of file MC_JETS.cc.
| AnalysisBuilder<MC_LEADINGJETS> plugin_MC_LEADINGJETS |
Definition at line 168 of file MC_LEADINGJETS.cc.
| AnalysisBuilder<MC_PHOTONJETS> plugin_MC_PHOTONJETS |
Definition at line 134 of file MC_PHOTONJETS.cc.
| AnalysisBuilder<MC_PHOTONJETUE> plugin_MC_PHOTONJETUE |
Definition at line 258 of file MC_PHOTONJETUE.cc.
| AnalysisBuilder<MC_SUSY> plugin_MC_SUSY |
Definition at line 320 of file MC_SUSY.cc.
| AnalysisBuilder<MC_TTBAR> plugin_MC_TTBAR |
Definition at line 150 of file MC_TTBAR.cc.
| AnalysisBuilder<MC_WJETS> plugin_MC_WJETS |
Definition at line 163 of file MC_WJETS.cc.
| AnalysisBuilder<MC_WPOL> plugin_MC_WPOL |
Definition at line 157 of file MC_WPOL.cc.
| AnalysisBuilder<MC_WWJETS> plugin_MC_WWJETS |
Definition at line 237 of file MC_WWJETS.cc.
| AnalysisBuilder<MC_XS> plugin_MC_XS |
| AnalysisBuilder<MC_ZJETS> plugin_MC_ZJETS |
Definition at line 116 of file MC_ZJETS.cc.
| AnalysisBuilder<MC_ZZJETS> plugin_MC_ZZJETS |
Definition at line 242 of file MC_ZZJETS.cc.
| AnalysisBuilder<OPAL_1993_S2692198> plugin_OPAL_1993_S2692198 |
Definition at line 196 of file OPAL_1993_S2692198.cc.
| AnalysisBuilder<OPAL_1998_S3780481> plugin_OPAL_1998_S3780481 |
Definition at line 198 of file OPAL_1998_S3780481.cc.
| AnalysisBuilder<OPAL_2001_S4553896> plugin_OPAL_2001_S4553896 |
Definition at line 159 of file OPAL_2001_S4553896.cc.
| AnalysisBuilder<OPAL_2004_S6132243> plugin_OPAL_2004_S6132243 |
Definition at line 263 of file OPAL_2004_S6132243.cc.
| AnalysisBuilder<PDG_HADRON_MULTIPLICITIES> plugin_PDG_HADRON_MULTIPLICITIES |
Definition at line 771 of file PDG_Hadron_Multiplicities.cc.
| AnalysisBuilder<PDG_HADRON_MULTIPLICITIES_RATIOS> plugin_PDG_HADRON_MULTIPLICITIES_RATIOS |
Definition at line 765 of file PDG_Hadron_Multiplicities_Ratios.cc.
| AnalysisBuilder<SFM_1984_S1178091> plugin_SFM_1984_S1178091 |
Definition at line 124 of file SFM_1984_S1178091.cc.
| AnalysisBuilder<STAR_2006_S6500200> plugin_STAR_2006_S6500200 |
Definition at line 115 of file STAR_2006_S6500200.cc.
| AnalysisBuilder<STAR_2006_S6860818> plugin_STAR_2006_S6860818 |
Definition at line 206 of file STAR_2006_S6860818.cc.
| AnalysisBuilder<STAR_2006_S6870392> plugin_STAR_2006_S6870392 |
Definition at line 91 of file STAR_2006_S6870392.cc.
| AnalysisBuilder<STAR_2008_S7869363> plugin_STAR_2008_S7869363 |
Definition at line 171 of file STAR_2008_S7869363.cc.
| AnalysisBuilder<STAR_2008_S7993412> plugin_STAR_2008_S7993412 |
Definition at line 83 of file STAR_2008_S7993412.cc.
| AnalysisBuilder<STAR_2009_UE_HELEN> plugin_STAR_2009_UE_HELEN |
Definition at line 168 of file STAR_2009_UE_HELEN.cc.
| AnalysisBuilder<TASSO_1990_S2148048> plugin_TASSO_1990_S2148048 |
Definition at line 167 of file TASSO_1990_S2148048.cc.
| AnalysisBuilder<UA1_1990_S2044935> plugin_UA1_1990_S2044935 |
Definition at line 179 of file UA1_1990_S2044935.cc.
| AnalysisBuilder<UA5_1982_S875503> plugin_UA5_1982_S875503 |
Definition at line 92 of file UA5_1982_S875503.cc.
| AnalysisBuilder<UA5_1986_S1583476> plugin_UA5_1986_S1583476 |
Definition at line 120 of file UA5_1986_S1583476.cc.
| AnalysisBuilder<UA5_1987_S1640666> plugin_UA5_1987_S1640666 |
Definition at line 73 of file UA5_1987_S1640666.cc.
| AnalysisBuilder<UA5_1988_S1867512> plugin_UA5_1988_S1867512 |
Definition at line 229 of file UA5_1988_S1867512.cc.
| AnalysisBuilder<UA5_1989_S1926373> plugin_UA5_1989_S1926373 |
Definition at line 113 of file UA5_1989_S1926373.cc.
| AnalysisBuilder<ZEUS_2001_S4815815> plugin_ZEUS_2001_S4815815 |
Definition at line 75 of file ZEUS_2001_S4815815.cc.
Definition at line 14 of file ParticleName.hh.
Referenced by ParticleNames::_particleId(), ALEPH_1991_S2435284::ALEPH_1991_S2435284(), ALEPH_1996_S3196992::ALEPH_1996_S3196992(), ALEPH_1996_S3486095::ALEPH_1996_S3486095(), ALEPH_2004_S5765862::ALEPH_2004_S5765862(), MC_SUSY::analyze(), BELLE_2006_S6265367::BELLE_2006_S6265367(), DELPHI_1995_S3137023::DELPHI_1995_S3137023(), DELPHI_1996_S3430090::DELPHI_1996_S3430090(), DELPHI_2002_069_CONF_603::DELPHI_2002_069_CONF_603(), H1_2000_S4129130::H1_2000_S4129130(), D0_2001_S4674421::init(), CDF_2008_S8095620::init(), CDF_2008_S7541902::init(), CDF_2006_S6653332::init(), JADE_1998_S3612880::JADE_1998_S3612880(), JADE_OPAL_2000_S4300807::JADE_OPAL_2000_S4300807(), OPAL_1993_S2692198::OPAL_1993_S2692198(), OPAL_1998_S3780481::OPAL_1998_S3780481(), OPAL_2001_S4553896::OPAL_2001_S4553896(), ParticleNames::ParticleNames(), PDG_HADRON_MULTIPLICITIES::PDG_HADRON_MULTIPLICITIES(), PDG_HADRON_MULTIPLICITIES_RATIOS::PDG_HADRON_MULTIPLICITIES_RATIOS(), TASSO_1990_S2148048::TASSO_1990_S2148048(), and ZEUS_2001_S4815815::ZEUS_2001_S4815815().
Definition at line 15 of file ParticleName.hh.
Referenced by Event::_geNormAlignment(), ParticleNames::_particleId(), ALICE_2010_S8624100::ALICE_2010_S8624100(), ALICE_2010_S8625980::ALICE_2010_S8625980(), ALICE_2010_S8706239::ALICE_2010_S8706239(), STAR_2006_S6860818::analyze(), ATLAS_2010_S8817804::ATLAS_2010_S8817804(), ATLAS_2011_S8924791::ATLAS_2011_S8924791(), ATLAS_2011_S9120807::ATLAS_2011_S9120807(), CDF_1988_S1865951::CDF_1988_S1865951(), CDF_1990_S2089246::CDF_1990_S2089246(), CDF_1993_S2742446::CDF_1993_S2742446(), CDF_1994_S2952106::CDF_1994_S2952106(), CDF_1996_S3108457::CDF_1996_S3108457(), CDF_1996_S3349578::CDF_1996_S3349578(), CDF_1996_S3418421::CDF_1996_S3418421(), CDF_1997_S3541940::CDF_1997_S3541940(), CDF_1998_S3618439::CDF_1998_S3618439(), CDF_2000_S4155203::CDF_2000_S4155203(), CDF_2000_S4266730::CDF_2000_S4266730(), CDF_2001_S4517016::CDF_2001_S4517016(), CDF_2001_S4563131::CDF_2001_S4563131(), CDF_2001_S4751469::CDF_2001_S4751469(), CDF_2002_S4796047::CDF_2002_S4796047(), CDF_2004_S5839831::CDF_2004_S5839831(), CDF_2005_S6080774::CDF_2005_S6080774(), CDF_2005_S6217184::CDF_2005_S6217184(), CDF_2006_S6450792::CDF_2006_S6450792(), CDF_2006_S6653332::CDF_2006_S6653332(), CDF_2007_S7057202::CDF_2007_S7057202(), CDF_2008_LEADINGJETS::CDF_2008_LEADINGJETS(), CDF_2008_NOTE_9351::CDF_2008_NOTE_9351(), CDF_2008_S7540469::CDF_2008_S7540469(), CDF_2008_S7541902::CDF_2008_S7541902(), CDF_2008_S7782535::CDF_2008_S7782535(), CDF_2008_S7828950::CDF_2008_S7828950(), CDF_2008_S8093652::CDF_2008_S8093652(), CDF_2008_S8095620::CDF_2008_S8095620(), CDF_2009_NOTE_9936::CDF_2009_NOTE_9936(), CDF_2009_S8057893::CDF_2009_S8057893::CDF_2009_S8057893(), CDF_2009_S8233977::CDF_2009_S8233977(), CDF_2009_S8383952::CDF_2009_S8383952(), CDF_2009_S8436959::CDF_2009_S8436959(), CDF_2010_S8591881_DY::CDF_2010_S8591881_DY(), CDF_2010_S8591881_QCD::CDF_2010_S8591881_QCD(), CMS_2011_S8957746::CMS_2011_S8957746(), D0_1996_S3214044::D0_1996_S3214044(), D0_1996_S3324664::D0_1996_S3324664(), D0_2001_S4674421::D0_2001_S4674421(), D0_2004_S5992206::D0_2004_S5992206(), D0_2006_S6438750::D0_2006_S6438750(), D0_2007_S7075677::D0_2007_S7075677(), D0_2008_S6879055::D0_2008_S6879055(), D0_2008_S7554427::D0_2008_S7554427(), D0_2008_S7662670::D0_2008_S7662670(), D0_2008_S7719523::D0_2008_S7719523(), D0_2008_S7837160::D0_2008_S7837160(), D0_2008_S7863608::D0_2008_S7863608(), D0_2009_S8202443::D0_2009_S8202443(), D0_2009_S8320160::D0_2009_S8320160(), D0_2009_S8349509::D0_2009_S8349509(), D0_2010_S8566488::D0_2010_S8566488(), D0_2010_S8570965::D0_2010_S8570965(), D0_2010_S8671338::D0_2010_S8671338(), E735_1998_S3905616::E735_1998_S3905616(), H1_1994_S2919893::H1_1994_S2919893(), H1_1995_S3167097::H1_1995_S3167097(), H1_2000_S4129130::H1_2000_S4129130(), STAR_2006_S6500200::init(), LHCB_2010_S8758301::LHCB_2010_S8758301(), ParticleNames::ParticleNames(), SFM_1984_S1178091::SFM_1984_S1178091(), STAR_2006_S6500200::STAR_2006_S6500200(), STAR_2006_S6860818::STAR_2006_S6860818(), STAR_2006_S6870392::STAR_2006_S6870392(), STAR_2008_S7869363::STAR_2008_S7869363(), STAR_2008_S7993412::STAR_2008_S7993412(), STAR_2009_UE_HELEN::STAR_2009_UE_HELEN(), UA1_1990_S2044935::UA1_1990_S2044935(), UA5_1986_S1583476::UA5_1986_S1583476(), UA5_1987_S1640666::UA5_1987_S1640666(), UA5_1988_S1867512::UA5_1988_S1867512(), UA5_1989_S1926373::UA5_1989_S1926373(), and ZEUS_2001_S4815815::ZEUS_2001_S4815815().
const double proton_mass_c2 = 938.27231 * MeV [static] |
Definition at line 50 of file Constants.hh.
Definition at line 96 of file Units.hh.
Referenced by _calcS(), JADE_1998_S3612880::analyze(), ExampleAnalysis::analyze(), BELLE_2006_S6265367::analyze(), JADE_1998_S3612880::finalize(), main(), AnalysisInfo::make(), mt2::mt2_massless(), and std::operator+=().
const double second = 1.e+9 *nanosecond [static] |
Definition at line 85 of file Units.hh.
Referenced by Sphericity::_calcSphericity(), UA5_1982_S875503::finalize(), EigenSystem< N >::getEigenVectors(), UA5_1982_S875503::init(), and D0_2010_S8570965::init().
Definition at line 54 of file ParticleName.hh.
Referenced by OPAL_1998_S3780481::analyze().
const double STP_Pressure = 1.*atmosphere [static] |
Definition at line 87 of file Constants.hh.
const double STP_Temperature = 273.15*kelvin [static] |
Definition at line 86 of file Constants.hh.
Definition at line 40 of file ParticleName.hh.
Referenced by IdentifiedFinalState::acceptChLeptons(), MC_HJETS::init(), and ParticleNames::ParticleNames().
const double teraelectronvolt = 1.e+3*gigaelectronvolt [static] |
const double TeV = teraelectronvolt [static] |
Definition at line 122 of file Units.hh.
Referenced by D0_2010_S8566488::analyze(), ATLAS_2010_S8894728::analyze(), ATLAS_2011_S8994773::init(), and ATLAS_2010_S8894728::init().
Definition at line 57 of file ParticleName.hh.
| const double TWOPI = 2*M_PI |
A pre-defined value of 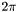 .
.
Definition at line 48 of file MathHeader.hh.
Referenced by _mapAngleM2PITo2Pi(), UA1_1990_S2044935::analyze(), STAR_2008_S7869363::analyze(), H1_1994_S2919893::analyze(), CDF_2009_S8233977::analyze(), CDF_1988_S1865951::analyze(), ALICE_2010_S8706239::analyze(), ATLAS_2010_S8918562::finalize(), ATLAS_2010_S8591806::finalize(), MC_ZZJETS::init(), MC_ZJETS::init(), MC_WWJETS::init(), MC_WJETS::init(), MC_HJETS::init(), MC_GENERIC::init(), mapAngle0To2Pi(), and mapAngleMPiToPi().
Definition at line 13 of file Constants.hh.
const double twopi_mc2_rcl2 [static] |
Definition at line 75 of file Constants.hh.
const double universe_mean_density = 1.e-25*g/cm3 [static] |
Definition at line 93 of file Constants.hh.
Definition at line 53 of file ParticleName.hh.
Referenced by OPAL_1998_S3780481::analyze().
const PdgId WMINUSBOSON = -24 [static] |
Definition at line 49 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames(), and WFinder::project().
const PdgId WPLUSBOSON = 24 [static] |
Definition at line 48 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames(), and WFinder::project().
Definition at line 36 of file ParticleName.hh.
Referenced by STAR_2006_S6860818::analyze(), and CMS_2011_S8978280::analyze().
Definition at line 37 of file ParticleName.hh.
Definition at line 50 of file ParticleName.hh.
Referenced by ParticleNames::ParticleNames(), ZFinder::project(), and InitialQuarks::project().